3.2: Circles

Circles

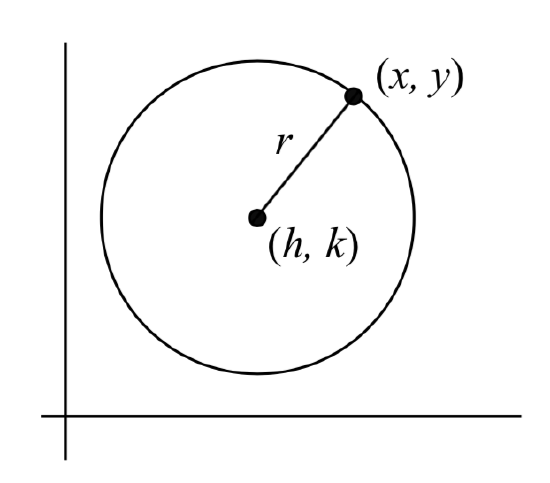
Recall from geometry that the definition of a circle is the set of points that are equidistant from a fixed point.

If we wanted to find an equation to represent a circle with a radius of $r$ centered at a point ($h$, $k$), we notice that the distance between any point ($x$, $y$) on the circle and the center point is always the same: $r$. Noting this, we can use our distance formula to write an equation for the radius:

$r=\sqrt{(x-h)^{2} +(y-k)^{2} }$

Squaring both sides of the equation gives us the standard equation for a circle.

Definition: The Standard Equation for a Circle

The equation of a circle centered at the point ($h$, $k$) with radius $r$ can be written as $$(x-h)^{2} +(y-k)^{2} =r^{2} \nonumber$$ Notice that a circle does not pass the vertical line test - it is not a function and it is not possible to write $y$ as a function of $x$ or vice versa.

Obtain the equation of a circle given a graph

Example $\PageIndex{1}$

Write an equation for the circle graphed here.

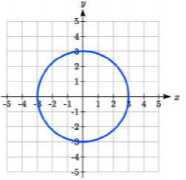
Solution

This circle is centered at the origin, the point (0, 0). By measuring horizontally or vertically from the center out to the circle, we can see the radius is 3. Using this information in our formula gives:

$$(x-0)^{2} +(y-0)^{2} =3^{2} \nonumber$$

simplified, this gives

$$x^{2} +y^{2} =9 \nonumber$$

Obtain the equation of a circle given a description.

Example $\PageIndex{2}$

Write an equation for a circle centered at the point (-3, 2) with radius 4.

Solution

Using the equation from above, $h = -3$, $k = 2$, and the radius $r = 4$. Using these in our formula,

$$(x-(-3))^{2} +(y-2)^{2} =4^{2} \nonumber$$

simplified, this gives

$$(x+3)^{2} +(y-2)^{2} =16 \nonumber$$

Example $\PageIndex{3}$

Write an equation for a circle with center (−2,3) and radius 5.

Solution.

Here, $(h,k) = (-2,3)$ and $r = 5$, so we get

$$\begin{array}{rcl} (x-(-2))^2+(y-3)^2 &= &(5)^2 \\ (x+2)^2+(y-3)^2 & = & 25 \end{array} \nonumber$$

Exercise $\PageIndex{4}$

Write an equation for a circle centered at (4, -2) with radius 6.

Answer

$$(x-4)^{2} +(y+2)^{2} =36\nonumber$$

Graph a circle given an equation. 

Example $\PageIndex{5}$:

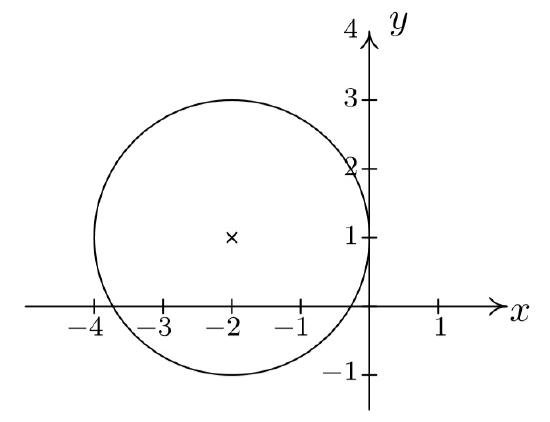
Graph $(x+2)^2+(y-1)^2 = 4$. Find the center and radius.

Solution

From the standard form of a circle we have that $x + 2$ is $x-h$, so $h = -2$ and $y - 1$ is $y - k$ so $k = 1$. This tells us that our center is $(-2,1)$. Furthermore, $r^2 = 4$, so $r = 2$. Thus we have a circle centered at $(-2,1)$ with a radius of $2$. Graphing gives us

$\Box$

Graph a circle given an equation that is not in standard form.

If we were to expand the equation in the previous example and gather up like terms, instead of the easily recognizable $(x+2)^2 + (y-1)^2 = 4$, we'd be contending with $x^2 + 4x + y^2 - 2y + 1 = 0.$ If we're given such an equation, we can complete the square in each of the variables to see if it fits the form of the Standard Equation of a circle by following the steps given below.

To Write the Equation of a Circle in Standard Form

1. Group the same variables together on one side of the equation and position the constant on the other side.
2. Complete the square on each variable.
3. Divide both sides by the coefficient of the squares. (For circles, the coefficients will be the same.)

Example $\PageIndex{6}$:

Complete the square to find the center and radius of $3x^2 - 6x + 3y^2 + 4y -4 = 0$.

Solution

$\begin{array}{rclr} 3x^2 - 6x + 3y^2 + 4y -4 & = & 0 & \\ 3x^2 - 6x + 3y^2 + 4y & = & 4 && \mbox{add \(4\) to both sides} \\ 3\left(x^2 - 2x \right) + 3\left(y^2 + \dfrac{4}{3} y\right) & = & 4 && \mbox{factor out leading coefficients} \\ 3\left(x^2 - 2x + \underline{1} \right) + 3\left(y^2 + \dfrac{4}{3} y + \underline{\underline{\dfrac{4}{9}}} \right) & = & 4 + 3\underline{(1)} + 3\underline{\underline{\left(\dfrac{4}{9}\right)}} && \mbox{complete the square in \(x\), \(y\)} \\ 3(x - 1)^2 + 3\left(y + \dfrac{2}{3}\right)^2 & = & \dfrac{25}{3} && \mbox{factor} \\ (x - 1)^2 + \left(y + \dfrac{2}{3}\right)^2 & = & \dfrac{25}{9} && \mbox{divide both sides by \(3\)}\end{array}$

From the standard form of the equation for a circle, we identify $x - 1$ as $x - h$, so $h = 1$, and $y + \frac{2}{3}$ as $y - k$, so $k = - \frac{2}{3}$. Hence, the center is $(h,k) = \left(1, -\frac{2}{3}\right)$. Furthermore, we see that $r^2 = \frac{25}{9}$ so the radius is $r = \frac{5}{3}$.

It is possible to obtain equations like $(x-3)^2 + (y+1)^2 = 0$ or $(x-3)^2 + (y+1)^2 = -1$, neither of which describes a circle. (Do you see why not?) The reader is encouraged to think about what, if any, points lie on the graphs of these two equations. 

Ellipses

An ellipse is an oval-shaped circle. In this section we will simplistically regard an ellipse as a squashed circle with a horizontal radius $a$ and a vertical radius $b$. The vertical radius can be larger or smaller than the horizontal radius. When the horizontal and vertical radii are the same length, the shape is a circle, rather than an ellipse. The formula for an ellipse centered at the origin is  $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$.  When we shift the graph right $h$ units and up $k$ units by replacing $x$ with $x – h$ and $y$ with $y – k$, similar to what we did when we learned transformations, we obtain the standard form of the ellipse.

Definition: EQUATION OF AN ELLIPSE CENTERED AT $(h,k)$ IN STANDARD FORM

The standard form for the equation of an ellipse centered at $(h, k)$  is $$\dfrac{(x - h)^2}{a^2} + \dfrac{(y - k)^2}{b^2} = 1 \nonumber$$ where $a$ is the length of the horizontal "radius", and $b$ is the length of the vertical "radius".  The four endpoints of the radii are called vertices. The horizontal diameter or horizontal axis is $2a$ The vertical diameter or vertical axis is $2b$.

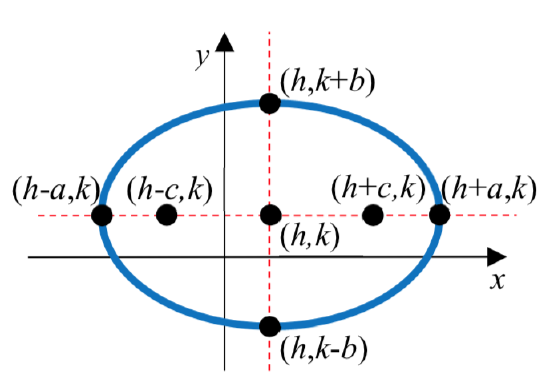Obtain the equation of an ellipse given a graph

Example $\PageIndex{7}$

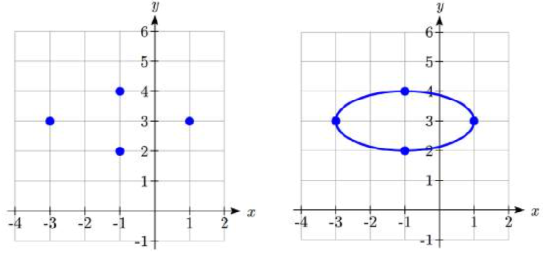
Find the standard form of the equation for the ellipse graphed here.

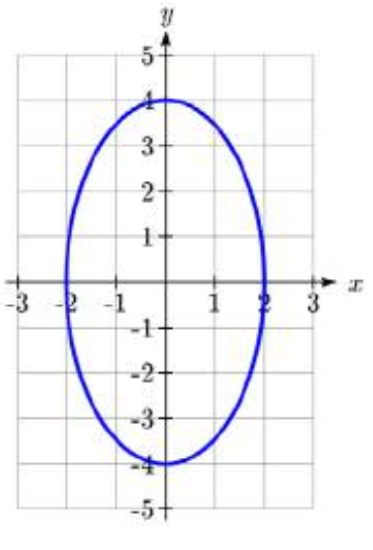
Solution

The center is at (0,0). From the graph we can see the horizontal radius is  $a = 2$ and the vertical radius is  $b = 4$.

The equation will be $$\dfrac{x^2}{2^2} + \dfrac{y^2}{4^2} = 1\text{ or }\dfrac{x^2}{4} + \dfrac{y^2}{16} = 1\nonumber$$

Obtain the equation of an ellipse given a description.

Example $\PageIndex{8}$

Find the standard form of the equation for an ellipse centered at (0,0) with horizontal radius of 16 and vertical radius of 8.

Solution

Since the center is at (0,0) , the horizontal radius is  $a = 14$ and the vertical radius is $b = 8$. The formula for the ellipse is then $$\dfrac{x^2}{16^2} + \dfrac{y^2}{8^2} = 1\text{ or }\dfrac{x^2}{256} + \dfrac{y^2}{64.} = 1\nonumber$$

Exercise $\PageIndex{9}$

Find the standard form of the equation for an ellipse centered at the origin with horizontal radius of 10 and vertical radius of 3.

Answer

$a =10$ and $b = 3$. $$\dfrac{x^2}{100} + \dfrac{y^2}{9} = 1\nonumber$$

Graph an ellipse given an equation. 

Example $\PageIndex{10}$

Put the equation of the ellipse $9{x^2} + {y^2} = 9$ in standard form. Find the lengths of the horizontal and vertical radii and sketch the graph.

Solution

The standard equation has a 1 on the right side, so this equation can be put in standard form by dividing by 9:

$$\dfrac{x^2}{1} + \dfrac{y^2}{9} = 1\nonumber$$

The horizontal radius is $\sqrt 1 =1$, the vertical radius is $\sqrt 9 =3$, and the center of the ellipse is at the origin.

To sketch the graph we locate the center and plot the location of the radii. Then we sketch the ellipse.

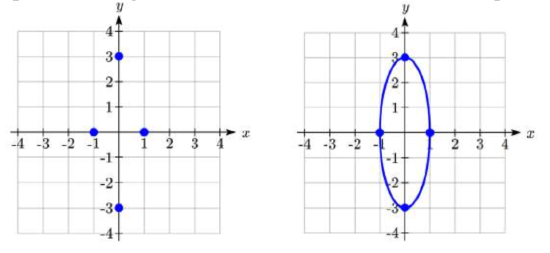
Exercise $\PageIndex{11}$

Find the center and horizontal and vertical radii for the ellipse $\left( x - 4 \right)^2 + \dfrac{\left( y + 2 \right)^2}{4} = 1$ and sketch the graph.

Answer

Center (4, -2) with $a = 1$, $b = 2$.
Vertices at (4 $\pm$ 1, -2) = (3,-2) and (5,-2) and (4, -2 $\pm$ 2) = (4, 0) and (4, -4).  (Graph unavailable)

Graph an ellipse given an equation that is not in standard form. 

Sometimes we are given the equation of an ellipse that is not in standard form. In this situation, completing the squre must be done twice to obtain the equation in standard form. 

Example $\PageIndex{12}$

Put the equation of the ellipse $x^2 + 2x + 4y^2 - 24y = - 33$ in standard form. Find the center and vertices, and sketch the graph.

Solution

To rewrite this in standard form, we will need to complete the square, twice.

Looking at the $x$ terms, $x^2 + 2x$, we like to have something of the form $(x + n)^2$. Notice that if we were to expand this, we’d get $x^2 + 2nx + n^2$, so in order for the coefficient on $x$ to match, we’ll need $(x + 1)^2 = x^2 + 2x + 1$. However, we don’t have $a +1$ on the left side of the equation to allow this factoring. To accommodate this, we will add 1 to both sides of the equation, which then allows us to factor the left side as a perfect square:

$$x^2 + 2x + 1 + 4y^2 - 24y = - 33 + 1\nonumber$$
$$(x + 1)^2 + 4y^2 - 24y = - 32\nonumber$$

Repeating the same approach with the $y$ terms, first we’ll factor out the 4.

$$4y^2 - 24y = 4(y^2 - 6y)\nonumber$$

Now we want to be able to write $4\left( y^2 - 6y \right)$ as

$$4(y + n)^2 = 4\left( y^2 + 2ny + n^2 \right)\nonumber$$

For the coefficient of $y$ to match, $n$ will have to -3, giving $4(y - 3)^2 = 4\left( y^2 - 6y + 9 \right) = 4y^2 - 24y + 36$.

To allow this factoring, we can add 36 to both sides of the equation.

$$(x + 1)^2 + 4y^2 - 24y + 36 = - 32 + 36\nonumber$$
$$(x + 1)^2 + 4\left( y^2 - 6y + 9 \right) = 4\nonumber$$
$$(x + 1)^2 + 4\left( y - 3 \right)^2 = 4\nonumber$$

Dividing by 4 gives the standard form of the equation for the ellipse

$$\dfrac{\left( x + 1 \right)^2}{4} + \dfrac{\left( y - 3 \right)^2}{1} = 1\nonumber$$

The center is at ($h$, $k$) = (-1, 3). The value of $a = \sqrt 4 = 2$ and the value of $b = \sqrt 1 = 1$.

To sketch the graph we locate the center and then locate the endpoints of the radii. Then we sketch the ellipse.