3.2: The Derivative as a Function

Last updated
Save as PDF

Page ID: 143970

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

Use the definition of the derivative to differentiate $f(x) = 2$.
Use the definition of the derivative to differentiate $g(x) = 3x - 4$.
Use the definition of the derivative to differentiate $h(x) = x^2$.
Use the definition of the derivative to differentiate $y = 2x^2 - x + 4$.
Use the definition of the derivative to differentiate $f(t) = t^3 - 5$.
Use the definition of the derivative to differentiate $g(t) = \sqrt{t}$.
Use the definition of the derivative to differentiate $h(t) = \sqrt{2 - 3t}$.
Use the definition of the derivative to differentiate $y = \dfrac{1}{x - 2}$.
Use the definition of the derivative to differentiate $f(x) = \dfrac{1}{x^2}$.
Use the definition of the derivative to differentiate $g(x) = \dfrac{1}{\sqrt{x + 1}}$.
Use the definition of the derivative to differentiate $h(x) = \left\{\begin{align*}
-x, && x \leq 0, \\
x^2, && x > 0.
\end{align*}\right.$
[Hint: Be careful at $x = 0$.]
Use the definition of the derivative to differentiate $f(x) = \left\{\begin{align*}
-x, && x \leq 0, \\
x^2 - x, && x > 0.
\end{align*}\right.$
[Hint: Be careful at $x = 0$.]
The graph of $g(x)$ is shown below. Sketch the graph of $g'(x)$.
$Graph of g(x) = 2.$
The graph of $h(x)$ is shown below. Sketch the graph of $h'(x)$.
$Graph of h(x) = -0.5x + 1.$
The graph of $f(x)$ is shown below. Sketch the graph of $\dfrac{df}{dx}$.
$Graph of f(x) = 0.5x^2 - x - 3.$
The graph of $g(x)$ is shown below. Sketch the graph of $\dfrac{dg}{dx}$.
$Graph of g(x) = -x * (x-1) * (x-3).$
The graph of $h(x)$ is shown below. Sketch the graph of $\dfrac{dh}{dx}$.
$Graph of h(x) = 0.2 * (x-2)^2 * (x+2)^2$
The graph of $f(x)$ is shown below. Sketch the graph of $f'(x)$.
$Graph of f(x) = -0.6 * (0.25x^4 - 1.5x^2 - 2x).$
The graph of $g(x)$ is shown below. Sketch the graph of $g'(x)$.
$Graph of g(x) = 3/(x^2 + 1).$
The graph of $h(x)$ is shown below. Sketch the graph of $h'(x)$.
$Graph of h(x) = sin(x) on the interval from -2*pi to 2*pi.$
The graph of $f(x)$ is shown below. Sketch the graph of $\dfrac{df}{dx}$.
$Graph of f(x) = |x|.$
The graph of $g(x)$ is shown below. Sketch the graph of $\dfrac{dg}{dx}$.
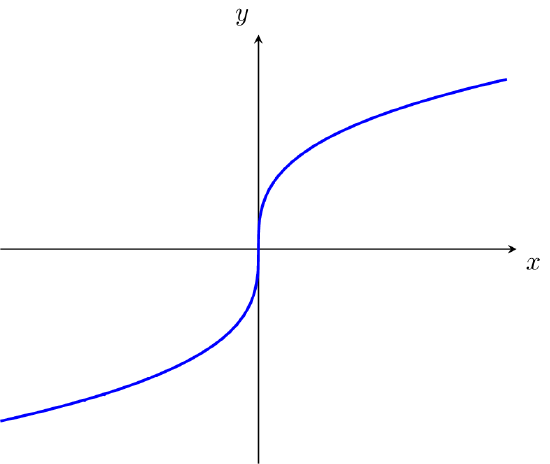
$Graph of g(x) = 2.5*x^(1/3).$
The graph of $h(x)$ is shown below. Sketch the graph of $\dfrac{dh}{dx}$.
$Graph of the function h(x). The function h(x) = x-1 for x < 0 and h(x) = x+1 for x >= 0.$
Use the graph of $f(x)$ below to answer the following.
1. List all values of $x$ for which $f(x)$ is not defined.
2. List all values of $x$ for which $\displaystyle \lim_{t \rightarrow x} f(t)$ does not exist.
3. List all values of $x$ for which $f(x)$ is not continuous.
4. List all values of $x$ for which $f(x)$ is not differentiable.
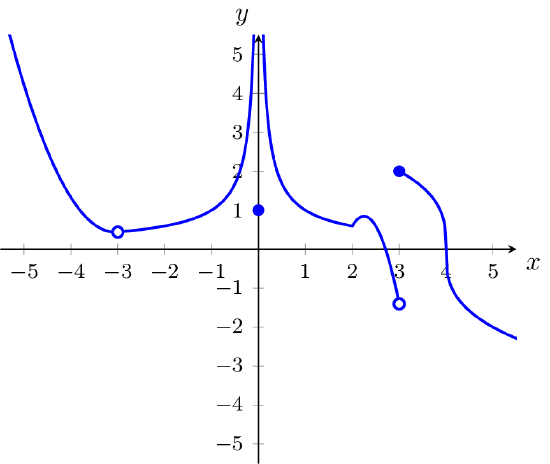
$The graph of the piecewise function f(x). Function f(x) = x^2 + 6.1097x + 9.7677 for x < -3; function f(x) = 1/|x|^(3/4) for -3 < x < 0; function f(x) = 1 at x = 0; function f(x) = 1/|x|^(3/4) for 0 < x <= 2; function f(x) = -4(x-2.25)^2 + 0.8446 for 2 < x < 3; and f(x) = -2(x-4)^(1/3) for x >= 3.$

Search

Text Color

Text Size

Margin Size

Font Type