6.2.2: Circles
- Page ID
- 88403
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)6.2.2 Learning Objectives
- Identify the radius and diameter of a circle.
- Use \(\pi\) or its approximate value in formulas.
- Find the circumference of a circle.
- Find the area of a circle.
- Find the perimeter or area of composite figures involving circles/
Circumference/Diameter/Radius
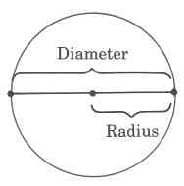
Definition: Part of a Circle
The circumference of a circle is the distance around the circle.
A diameter of a circle is any line segment that passes through the center of the circle and has its endpoints on the circle.
A radius of a circle is any line segment having as its endpoints the center of the circle and a point on the circle.
The radius is one half the diameter.
The Number \(\pi\)
The symbol \(\pi\), read "pi," represents the nonterminating, nonrepeating decimal number 3.14159 … . This number has been computed to millions of decimal places without the appearance of a repeating block of digits.
For computational purposes, \(\pi\) is often approximated as 3.14. We will write \(\pi \approx 3.14\) to denote that \(\pi\) is approximately equal to 3.14. The symbol "≈" means "approximately equal to." Use the \(\pi\) key on your calculator when evaluating for the best approximation.
Formulas
To find the circumference of a circle, we need only know its diameter or radius. We then use a formula for computing the circumference of the circle.
Definition: Formula
A formula is a rule or method for performing a task. In mathematics, a formula is a rule that directs us in computations.
Formulas are usually composed of letters that represent important, but possibly unknown, quantities.
If \(C, d\), and \(r\) represent, respectively, the circumference, diameter, and radius of a circle, then the following two formulas give us directions for computing the circumference of the circle.
Circumference Formulas
- \(C = \pi d\)
- \(C = 2 \pi r\)
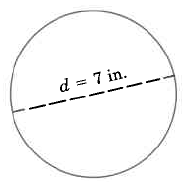
Example 1
Find the exact circumference of the circle.
Solution
Use the formula \(C = \pi d\).
\(C = \pi \cdot 7\text{ in}\)
By commutativity of multiplication,
\(C = 7\text{ in} \cdot \pi\)
\(C = 7 \pi \text{ in}\), exactly
This result is exact since \(\pi\) has not been approximated.
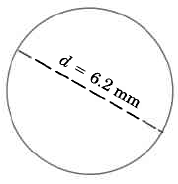
Example 2
Find the approximate circumference of the circle.
Solution
Use the formula \(C = \pi d\).
\(C \approx (3.14)(6.2)\)
\(C \approx 19.648 \text{ mm}\)
This result is approximate since \(\pi\) has been approximated by 3.14.
Example 3
Find the approximate circumference of a circle with radius 18 inches.
Solution
Since we're given that the radius, \(r\), is 18 in, we'll use the formula \(C = 2\pi r\).
\(C \approx (2)(3.14)(18 \text{ in})\)
\(C \approx 113.04 \text{ in}\)
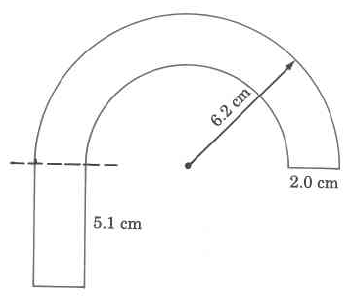
Example 4
Find the approximate area of the figure.
Solution
We notice that we have two semicircles (half circles).
The larger radius is 6.2 cm.
The smaller radius is \(\text{6.2 cm - 2.0 cm = 4.2 cm.}\)
The width of the bottom part of the rectangle is 2.0 cm.
\(\begin{array} {rcll} {\text{Perimeter}} & = & {\text{2.0 cm}} & {} \\ {} & & {\text{5.1 cm}} & {} \\ {} & & {\text{2.0 cm}} & {} \\ {} & & {\text{5.1 cm}} & {} \\ {} & & {(0.5) \cdot (2) \cdot (3.14) \cdot \text{(6.2 cm)}} & {\text{Circumference of outer semicircle.}} \\ {} & \ \ + & {\underline{(0.5) \cdot (2) \cdot (3.14) \cdot \text{(4.2 cm)}}} & {\text{Circumference of inner semicircle.}} \\ {} & & {} & {\text{6.2 cm - 2.0 cm = 4.2 cm}} \\ {} & & {} & {\text{The 0.5 appears because we want the}} \\ {} & & {} & {\text{perimeter of only half a circle.}} \end{array}\)
\(\begin{array} {rcr} {\text{Perimeter}} & \approx & {\text{2.0 cm}} \\ {} & & {\text{5.1 cm}} \\ {} & & {\text{2.0 cm}} \\ {} & & {\text{5.1 cm}} \\ {} & & {\text{19.468 cm}} \\ {} & & {\underline{\text{+13.188 cm}}} \\ {} & & {\text{48.856 cm}} \end{array}\)
Try It Now 1
Find the exact circumference of the circle.
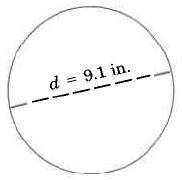
- Answer
-
\(9.1 \pi\) in
Try It Now 2
Find the approximate circumference of the circle.
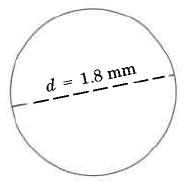
- Answer
-
5.652 mm
Try It Now 3
Find the approximate circumference of the circle with radius 20.1 m.
- Answer
-
126.228 m
Try It Now 4
Find the approximate outside perimeter of
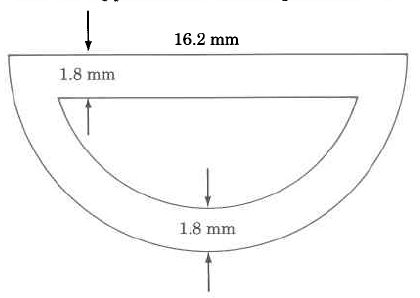
- Answer
-
41.634 mm
Area of a Circle
| Figure | Area Formula | Statement | |
 |
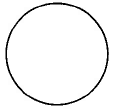Circle | \(A_c = \pi r^2\) | Area of a circle is \(\pi\) times the square of the radius. |
Example 5
Find the approximate area of the circle.
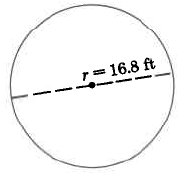
Solution
\(\begin{array} {rcl} {A_c} & = & {\pi \cdot r^2} \\ {} & \approx & {(3.14) \cdot (16.8 \text{ ft})^2} \\ {} & \approx & {(3.14) \cdot (\text{282.24 sq ft})} \\ {} & \approx & {888.23 \text{ sq ft}} \end{array}\)
The area of this circle is approximately 886.23 sq ft.
Example 6
Find the approximate area of the circle.
Solution
In this case we are given the diameter instead of the radius. We need to find the radius before we can calculate the area.
\(r=\dfrac{d}{2}=\dfrac{6.2}{2}=3.1 \text{mm}\)
\(\begin{array} {rcl} {A_c} & = & {\pi \cdot r^2} \\ {} & \approx & {(3.14) \cdot (6.2 \text{ ft})^2} \\ {} & \approx & {(3.14) \cdot (\text{38.44 sq mm})} \\ {} & \approx & {120.7 \text{ sq mm}} \end{array}\)
The area of this circle is approximately 120.7 sq mm.
Example 4
Find the approximate area of the figure.
Solution
We notice that we have two semicircles (half circles) and a small rectangle
The larger radius is 6.2 cm.
The smaller radius is \(\text{6.2 cm - 2.0 cm = 4.2 cm.}\)
The width of the bottom part of the rectangle is 2.0 cm.
The area of this shape will be \(A= \text{area of the rectangle}+\text{area of the outer semicircle}-\text{area of the inner semicircle}\)
Area of the rectangle: \(A=5.1\cdot 2=10.2 \text{ cm}\)
Area of the outer semicircle \(A=\dfrac{ \pi (6.2)^2}{2}=9.7 \text{ cm}\)
Area of the inner semicircle \(A=\dfrac{ \pi (4.2)^2}{2}=6.6 \text{ cm}\)
\(A= \text{area of the rectangle}+\text{area of the outer semicircle}-\text{area of the inner semicircle}=10.2 \text{cm}+9.7 \text{cm}- 6.6 \text{cm}=13.3 \text{cm}\)