7.9: The Period of the Nonlinear Pendulum
- Page ID
- 91095
RECALL THAT THE PERIOD OF THE SIMPLE PENDULUM is given by
\[T=\dfrac{2 \pi}{\omega}=2 \pi \sqrt{\dfrac{L}{g}} \nonumber \]
for
\[\omega \equiv \sqrt{\dfrac{g}{L}} \nonumber \]
This was based upon the solving the linear pendulum Equation 7.5.2. This equation was derived assuming a small angle approximation. How good is this approximation? What is meant by a small angle?
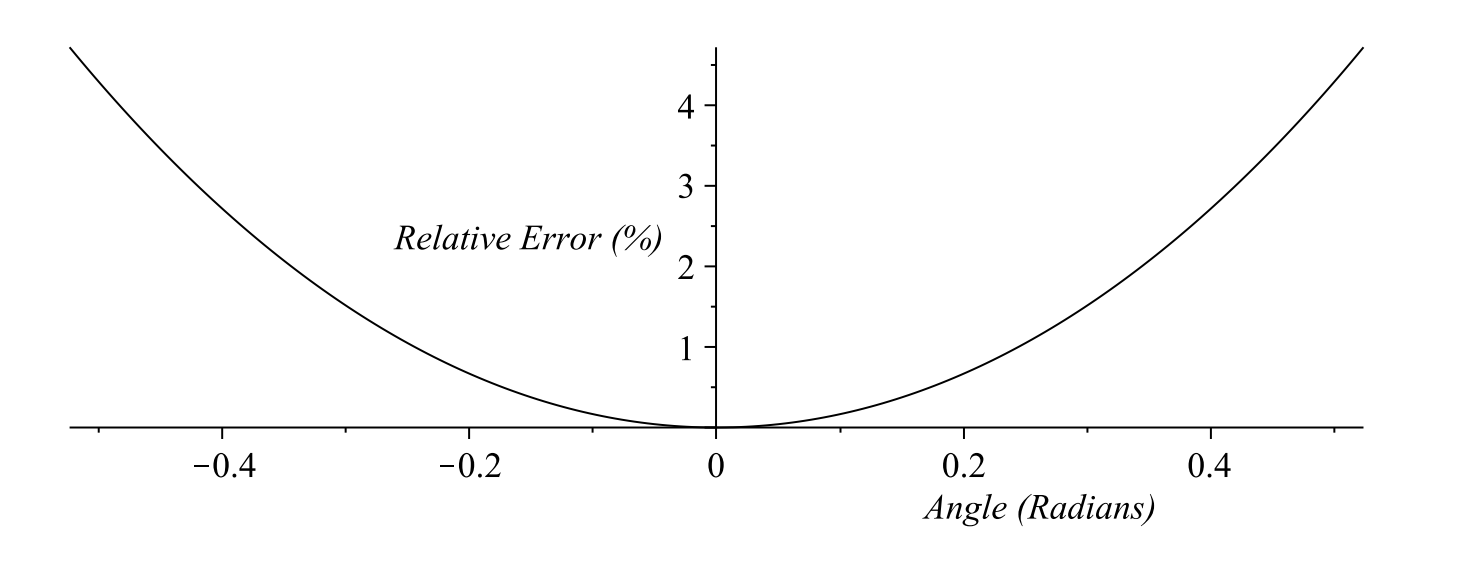
We recall that the Taylor series approximation of \(\sin \theta\) about \(\theta=0\) :
\[\sin \theta=\theta-\dfrac{\theta^{3}}{3 !}+\dfrac{\theta^{5}}{5 !}+\ldots \nonumber \]
One can obtain a bound on the error when truncating this series to one term after taking a numerical analysis course. But we can just simply plot the relative error, which is defined as
\[\text { Relative Error }=\left|\dfrac{\sin \theta-\theta}{\sin \theta}\right| \nonumber. \nonumber \]
A plot of the relative error is given in Figure \(\PageIndex{1}\). Thus for \(\theta \approx 0.4\) radians
\(\left(\right.\) or, \(\left.23^{\circ}\right)\) we have that the relative error is about \(2.6 \%\).
(Relative error in \(\sin \theta\) approximation). We would like to do better than this. So, we now turn to the nonlinear pendulum equation 7.5.1 in the simpler form
\[\ddot{\theta}+\omega^{2} \sin \theta=0 \nonumber \]
(Solution of nonlinear pendulum equation). We next employ a technique that is useful for equations of the form
\[\ddot{\theta}+F(\theta)=0 \nonumber \]
when it is easy to integrate the function \(F(\theta)\). Namely, we note that
\[\dfrac{d}{d t}\left[\dfrac{1}{2} \dot{\theta}^{2}+\int^{\theta(t)} F(\phi) d \phi\right]=(\ddot{\theta}+F(\theta)) \dot{\theta}\nonumber \]
For the nonlinear pendulum problem, we multiply Equation \(\PageIndex{4}\) by \(\dot{\theta}\),
\[\ddot{\theta} \dot{\theta}+\omega^{2} \sin \theta \dot{\theta}=0 \nonumber \]
and note that the left side of this equation is a perfect derivative. Thus,
\[\dfrac{d}{d t}\left[\dfrac{1}{2} \dot{\theta}^{2}-\omega^{2} \cos \theta\right]=0 \nonumber \]
Therefore, the quantity in the brackets is a constant. So, we can write
\[\dfrac{1}{2} \dot{\theta}^{2}-\omega^{2} \cos \theta=c \nonumber \]
Solving for \(\dot{\theta}\), we obtain
\[\dfrac{d \theta}{d t}=\sqrt{2\left(c+\omega^{2} \cos \theta\right)}\nonumber \]
This equation is a separable first order equation and we can rearrange and integrate the terms to find that
\[t=\int d t=\int \dfrac{d \theta}{\sqrt{2\left(c+\omega^{2} \cos \theta\right)}}\nonumber \]
Of course, we need to be able to do the integral. When one finds a solution in this implicit form, one says that the problem has been solved by quadratures. Namely, the solution is given in terms of some integral.
In fact, the above integral can be transformed into what is known as an elliptic integral of the first kind. We will rewrite this result and then use it to obtain an approximation to the period of oscillation of the nonlinear pendulum, leading to corrections to the linear result found earlier.
We will first rewrite the constant found in Equation \(\PageIndex{5}\). This requires a little physics. The swinging of a mass on a string, assuming no energy loss at the pivot point, is a conservative process. Namely, the total mechanical energy is conserved. Thus, the total of the kinetic and gravitational potential energies is a constant. The kinetic energy of the mass on the string is given as
\[T=\dfrac{1}{2} m v^{2}=\dfrac{1}{2} m L^{2} \dot{\theta}^{2}\nonumber \]
The potential energy is the gravitational potential energy. If we set the potential energy to zero at the bottom of the swing, then the potential energy is \(U=m g h\), where \(h\) is the height that the mass is from the bottom of the swing. A little trigonometry gives that \(h=L(1-\cos \theta) .\) So,
\[U=m g L(1-\cos \theta) \nonumber \]
(Total mechanical energy for the nonlinear pendulum). So, the total mechanical energy is
\[E=\dfrac{1}{2} m L^{2} \dot{\theta}^{2}+m g L(1-\cos \theta) \nonumber \]
We note that a little rearranging shows that we can relate this result to Equation Equation \(\PageIndex{5}\). Dividing by \(m\) and \(L^{2}\) and using the definition of \(\omega^{2}=g / L\), we have
\[\dfrac{1}{2} \dot{\theta}^{2}-\omega^{2} \cos \theta=\dfrac{1}{m L^{2}} E-\omega^{2} \nonumber \]
Therefore, we have determined the integration constant in terms of the total mechanical energy,
\[c=\dfrac{1}{m L^{2}} E-\omega^{2} \nonumber \]
We can use Equation \(\PageIndex{6}\) to get a value for the total energy. At the top of the swing the mass is not moving, if only for a moment. Thus, the kinetic energy is zero and the total mechanical energy is pure potential energy. Letting \(\theta_{0}\) denote the angle at the highest angular position, we have that
\[E=m g L\left(1-\cos \theta_{0}\right)=m L^{2} \omega^{2}\left(1-\cos \theta_{0}\right) \nonumber \]
Therefore, we have found that
\[\dfrac{1}{2} \dot{\theta}^{2}-\omega^{2} \cos \theta=-\omega^{2} \cos \theta_{0} \nonumber \]
We can solve for \(\dot{\theta}\) and integrate the differential equation to obtain
\[t=\int d t=\int \dfrac{d \theta}{\omega \sqrt{2\left(\cos \theta-\cos \theta_{0}\right)}}\nonumber \]
Using the half angle formula,
\[\sin ^{2} \dfrac{\theta}{2}=\dfrac{1}{2}(1-\cos \theta)\nonumber \]
we can rewrite the argument in the radical as
\[\cos \theta-\cos \theta_{0}=2\left[\sin ^{2} \dfrac{\theta_{0}}{2}-\sin ^{2} \dfrac{\theta}{2}\right] \nonumber \]
Noting that a motion from \(\theta=0\) to \(\theta=\theta_{0}\) is a quarter of a cycle, we have that
\[T=\dfrac{2}{\omega} \int_{0}^{\theta_{0}} \dfrac{d \theta}{\sqrt{\sin ^{2} \dfrac{\theta_{0}}{2}-\sin ^{2} \dfrac{\theta}{2}}} \nonumber \]
This result can now be transformed into an elliptic integral. \({ }^{1}\) We define
\[z=\dfrac{\sin \dfrac{\theta}{2}}{\sin \dfrac{\theta_{0}}{2}} \nonumber \]
and
\[k=\sin \dfrac{\theta_{0}}{2}\nonumber \]
Then, Equation \(\PageIndex{8}\) becomes
\[T=\dfrac{4}{\omega} \int_{0}^{1} \dfrac{d z}{\sqrt{\left(1-z^{2}\right)\left(1-k^{2} z^{2}\right)}} \nonumber \]
This is done by noting that \(d z=\dfrac{1}{2 k} \cos \dfrac{\theta}{2} d \theta=\dfrac{1}{2 k}\left(1-k^{2} z^{2}\right)^{1 / 2} d \theta\) and that \(\sin ^{2} \dfrac{\theta_{0}}{2}-\sin ^{2} \dfrac{\theta}{2}=k^{2}\left(1-z^{2}\right)\). The integral in this result is called the complete elliptic integral of the first kind.
- 1
-
Elliptic integrals were first studied by Leonhard Euler and Giulio Carlo de’ Toschi di Fagnano \((1682-1766)\), who studied the lengths of curves such as the ellipse and the lemniscate,
\[\left(x^{2}+y^{2}\right)^{2}=x^{2}-y^{2}. \nonumber \]
We note that the incomplete elliptic integral of the first kind is defined as
\[F(\phi, k) \equiv \int_{0}^{\phi} \dfrac{d \theta}{\sqrt{1-k^{2} \sin ^{2} \theta}}=\int_{0}^{\sin \phi} \dfrac{d z}{\sqrt{\left(1-z^{2}\right)\left(1-k^{2} z^{2}\right)}} \nonumber \]
(The complete and incomplete elliptic integrals of the first kind). Then, the complete elliptic integral of the first kind is given by \(K(k)= F(\dfrac{\pi}{2}, k)\), or
\[K(k)=\int_{0}^{\pi / 2} \dfrac{d \theta}{\sqrt{1-k^{2} \sin ^{2} \theta}}=\int_{0}^{1} \dfrac{d z}{\sqrt{\left(1-z^{2}\right)\left(1-k^{2} z^{2}\right)}} \nonumber \]
Therefore, the period of the nonlinear pendulum is given by
\[T=\dfrac{4}{\omega} K\left(\sin \dfrac{\theta_{0}}{2}\right) \nonumber \]
There are table of values for elliptic integrals. However, one can use a computer algebra system to compute values of such integrals. We will look for small angle approximations.
For small angles \(\left(\theta_{0} \ll \dfrac{\pi}{2}\right)\), we have that \(k\) is small. So, we can develop a series expansion for the period, \(T\), for small \(k\). This is simply done by using the binomial expansion,
\[\left(1-k^{2} z^{2}\right)^{-1 / 2}=1+\dfrac{1}{2} k^{2} z^{2}+\dfrac{3}{8} k^{2} z^{4}+O\left((k z)^{6}\right)\nonumber \]
Inserting this expansion into the integrand for the complete elliptic integral and integrating term by term, we find that
\[T=2 \pi \sqrt{\dfrac{L}{g}}\left[1+\dfrac{1}{4} k^{2}+\dfrac{9}{64} k^{4}+\ldots\right] \nonumber \]
The first term of the expansion gives the well known period of the simple pendulum for small angles. The next terms in the expression give further corrections to the linear result which are useful for larger amplitudes of oscillation. In Figure \(\PageIndex{2}\), we show the relative errors incurred when keeping the \(k^{2}\) (quadratic) and \(k^{4}\) (quartic) terms as compared to the exact value of the period.
