Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

11.6: Circular Functions

Last updated

Mar 4, 2023
Save as PDF
- 11.5: Radians
- 11.7: More Functions and Identities

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

7.1 Transformations of Graphs

Homework 7-1

1. amplitude 2, period $2\pi$ , midline $y=-3$

3. amplitude 1, period $\dfrac{\pi}{2}$ , midline $y=0$

5. amplitude 5, period $6\pi$ , midline $y=0$

7. amplitude 1, period 2, midline $y=1$

9. $Screen Shot 2023-02-25 at 1.36.36 PM.png$

11. $Screen Shot 2023-02-25 at 1.36.43 PM.png$

13. $Screen Shot 2023-02-25 at 1.36.51 PM.png$

15. $Screen Shot 2023-02-25 at 1.36.58 PM.png$

17. $y=-2 \sin x$

19. $y=-2 \cos x$

21. $y=-0.75 \cos x$

23.

a amplitude 2, period $\dfrac{2\pi}{3}$ , midline $y=0$

b $y = -2\sin 3x$

25.

a amplitude 3, period $2\pi$ , midline $y=0$

b $y = 3 \sin \dfrac{x}{2}$

27.

a amplitude 0.5, period $4\pi$ , midline $y = 3.5$

b $y = 0.5 \cos \dfrac{x}{2} + 3.5$

29.

a amplitude 2, period 4, midline $y=-1$

b $y = -1 + 2 \sin \dfrac{\pi x}{2}$

31.

$t$	$2t$	$\cos 2t$	$-5 \cos 2t$	$2 - 5\cos 2t$
0	0	1	-5	-3
$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	0	0	2
$\dfrac{\pi}{2}$	$\pi$	-1	5	7
$\dfrac{3\pi}{4}$	$\dfrac{3\pi}{2}$	0	0	2
$\pi$	$2\pi$	1	-5	-3

b $Screen Shot 2023-02-25 at 1.43.53 PM.png$

33.

$t$	$\dfrac{t}{2}$	$\cos \dfrac{t}{2}$	$3 \cos \dfrac{t}{2}$	$1 + 3 \cos \dfrac{t}{2}$
0	0	1	3	4
$\pi$	$\dfrac{\pi}{2}$	0	0	1
$2\pi$	$\pi$	-1	-3	-2
$3\pi$	$\dfrac{3\pi}{2}$	0	0	1
$4\pi$	$2\pi$	1	3	4

b $Screen Shot 2023-02-25 at 1.46.33 PM.png$

35.

$t$	$\dfrac{t}{3}$	$\sin \dfrac{t}{3}$	$2\sin \dfrac{t}{3}$	$-3 + 2 \sin \dfrac{t}{3}$
0	0	0	0	-3
$\dfrac{3\pi}{2}$	$\dfrac{\pi}{2}$	1	2	-1
$3\pi$	$\pi$	0	0	-3
$\dfrac{9\pi}{2}$	$\dfrac{3\pi}{2}$	-1	-2	-5
$6\pi$	$2\pi$	0	0	-3

39. $Screen Shot 2023-02-25 at 1.51.08 PM.png$

41. $Screen Shot 2023-02-25 at 1.51.18 PM.png$

43. $Screen Shot 2023-02-25 at 1.51.30 PM.png$

45.

a $Screen Shot 2023-02-25 at 1.51.40 PM.png$

b $W(t) = 12 + 8 \cos \left( \dfrac{\pi t}{6} \right)$

47.

a 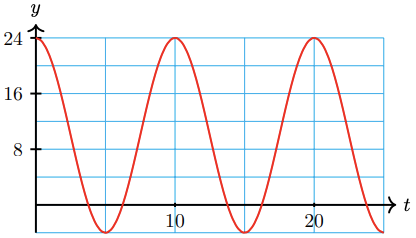$Screen Shot 2023-02-25 at 1.51.49 PM.png$

b $h = 10 + 14 \cos \left( \dfrac{\pi t}{5} \right)$

49. $H=12-2.4 \cos \left(\dfrac{\pi t}{6}\right)$

51. $y=155 \cos (120 \pi t)$

53.

a $Screen Shot 2023-02-25 at 1.57.44 PM.png$

b period $\dfrac{\pi}{2}$ , midline $y = 0$

55.

a 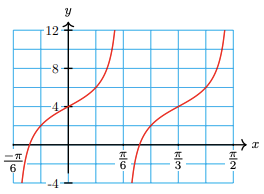$Screen Shot 2023-02-25 at 1.57.57 PM.png$

b period $\dfrac{\pi}{3}$ , midline $y=4$

57.

a $Screen Shot 2023-02-25 at 1.58.12 PM.png$

b period $4 \pi$ , midline $y=3$

59. $\dfrac{\pi}{12}, \dfrac{5\pi}{12}, \dfrac{7\pi}{12}, \dfrac{11\pi}{12}, \dfrac{13\pi}{12}, \dfrac{17\pi}{12}, \dfrac{19\pi}{12}, \dfrac{23\pi}{12}$

61. $\dfrac{7\pi}{12}, \frac{11\pi}{12}, \dfrac{19\pi}{12}, \dfrac{23\pi}{12}$

63. $\dfrac{\pi}{12}, \dfrac{5 \pi}{12}, \dfrac{3 \pi}{4}, \dfrac{13 \pi}{12}, \dfrac{17 \pi}{12}, \dfrac{7 \pi}{4}$

65. 1.83, 2.88, 4.97, 6.02

67. 4.19

69. 0.28, 1.81, 2.37, 3.91, 4.47, 6.00

7.2 The General Sinusoidal Function

Homework 7-2

$x$

$-\pi$

$\dfrac{-5\pi}{6}$

$\dfrac{-2\pi}{3}$

$\dfrac{-\pi}{2}$

$\dfrac{-\pi}{3}$

$\dfrac{-\pi}{6}$

$\dfrac{\pi}{6}$

$\dfrac{\pi}{3}$

$\dfrac{\pi}{2}$

$\dfrac{2\pi}{3}$

$\dfrac{5\pi}{6}$

$\pi$

$f(x)$

$\dfrac{-1}{2}$

$\dfrac{-\sqrt{3}}{2}$

-1

$\dfrac{-\sqrt{3}}{2}$

$\dfrac{-1}{2}$

$\dfrac{1}{2}$

$\dfrac{\sqrt{3}}{2}$

$\dfrac{1}{2}$

$g(x)$

$\dfrac{\sqrt{3}}{2}$

$\dfrac{1}{2}$

$\dfrac{-1}{2}$

$\dfrac{-\sqrt{3}}{2}$

-1

$\dfrac{-\sqrt{3}}{2}$

$\dfrac{-1}{2}$

$\dfrac{1}{2}$

$\dfrac{\sqrt{3}}{2}$

b $Screen Shot 2023-02-25 at 2.11.38 PM.png$

c $\dfrac{\pi}{3}$ to the right

d $\dfrac{5\pi}{6}$

e $\dfrac{-2\pi}{3}, \dfrac{\pi}{3}$

$x$	$-\pi$	$\dfrac{-3\pi}{4}$	$\dfrac{-\pi}{2}$	$\dfrac{-\pi}{4}$	0	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\dfrac{3\pi}{4}$	$\pi$
$f(x)$	0	1	undef	-1	0	1	undef	-1	0
$g(x)$	1	undef	-1	0	1	undef	-1	0	1

b $Screen Shot 2023-02-25 at 3.36.35 PM.png$

c $\dfrac{\pi}{4}$ to the left

d $-\pi, 0, \pi$

e $\dfrac{-\pi}{4}, \dfrac{-3\pi}{4}$

a amplitude 2, shift $\dfrac{\pi}{6}$ to the left

$x$	$x + \dfrac{\pi}{6}$	$\cos \left( x + \dfrac{\pi}{6} \right)$	$-2 \cos \left( x+ \dfrac{\pi}{6} \right)$
$\dfrac{-7\pi}{6}$	$-\pi$	-1	2
$\dfrac{-2\pi}{3}$	$\dfrac{-\pi}{2}$	0	0
$\dfrac{-\pi}{6}$	0	1	-2
$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	0	0
$\dfrac{5\pi}{6}$	$\pi$	-1	2
$\dfrac{4\pi}{3}$	$\dfrac{3\pi}{2}$	0	0
$\dfrac{11\pi}{6}$	$2\pi$	1	-2

c 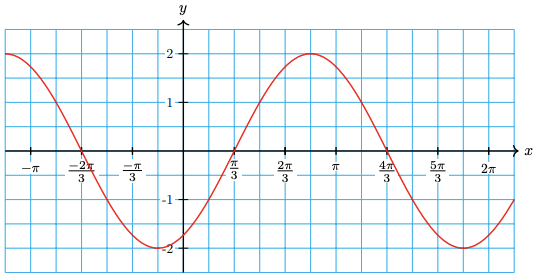$Screen Shot 2023-02-25 at 3.41.47 PM.png$

d $\dfrac{\pi}{2}, \dfrac{7\pi}{6}$

e $\dfrac{\pi}{3}, \dfrac{4\pi}{3}$

a $f(x)=\sin \left(x+\dfrac{\pi}{4}\right)$

b $f(x)=\cos \left(x-\dfrac{\pi}{4}\right)$

a $f(x)=\tan \left(x-\dfrac{\pi}{3}\right)$

b $f(x)=\tan \left(x+\dfrac{2 \pi}{3}\right)$

11.

a period $\pi$ , shift $\frac{\pi}{6}$ to the right

$x$	$2x$	$2x - \dfrac{\pi}{3}$	$\cos \left( 2x - \dfrac{\pi}{3} \right)$
$\dfrac{\pi}{6}$	$\dfrac{\pi}{3}$	0	1
$\dfrac{5\pi}{12}$	$\dfrac{5\pi}{6}$	$\dfrac{\pi}{2}$	0
$\dfrac{2\pi}{3}$	$\dfrac{4\pi}{3}$	$\pi$	-1
$\dfrac{11\pi}{12}$	$\dfrac{11\pi}{6}$	$\dfrac{3\pi}{2}$	0
$\dfrac{7\pi}{6}$	$\dfrac{7\pi}{3}$	$2\pi$	1

c $Screen Shot 2023-02-25 at 3.47.31 PM.png$

d $\dfrac{\pi}{6}, \dfrac{7 \pi}{6}$

e $\dfrac{5 \pi}{12}, \dfrac{11 \pi}{12}, \dfrac{13 \pi}{6}, \dfrac{23 \pi}{12}$

13.

a period 2, shift $\frac{1}{3}$ to the left

$x$	$\pi x$	$\pi x + \dfrac{\pi}{3}$	$\sin \left( \pi x + \dfrac{\pi}{3} \right)$
$\dfrac{-1}{3}$	$\dfrac{-\pi}{3}$	0	0
$\dfrac{1}{6}$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{2}$	1
$\dfrac{2}{3}$	$\dfrac{2\pi}{3}$	$\pi$	0
$\dfrac{7}{6}$	$\dfrac{7\pi}{6}$	$\dfrac{3\pi}{2}$	-1
$\dfrac{5}{3}$	$\dfrac{5\pi}{3}$	$2\pi$	0

c $Screen Shot 2023-02-25 at 3.53.01 PM.png$

d $\dfrac{-11}{6}, \dfrac{1}{6}$

e $\dfrac{-4}{3}, \dfrac{-1}{3}, \dfrac{2}{3}, \dfrac{5}{3}$

15.

a midline $y=4$ , period $4 \pi$ , horizontal shift $\frac{\pi}{3}$ to the right, amplitude 3

$x$	$\dfrac{x}{2}$	$\dfrac{x}{2} - \dfrac{\pi}{6}$	$\sin \left( \dfrac{x}{2} - \dfrac{\pi}{6} \right)$	$3 \sin \left( \dfrac{x}{2} - \dfrac{\pi}{6} \right) + 4$
$\dfrac{\pi}{3}$	$\dfrac{\pi}{6}$	0	0	4
$\dfrac{4\pi}{3}$	$\dfrac{2\pi}{3}$	$\dfrac{\pi}{2}$	1	7
$\dfrac{7\pi}{3}$	$\dfrac{7\pi}{6}$	$\pi$	0	3
$\dfrac{10\pi}{3}$	$\dfrac{5\pi}{3}$	$\dfrac{3\pi}{2}$	-1	1
$\dfrac{13\pi}{3}$	$\dfrac{13\pi}{6}$	$2\pi$	0	4

c $Screen Shot 2023-02-25 at 4.12.20 PM.png$

d no solution for $0 \leq x \leq 2 \pi$

e $\dfrac{\pi}{3}$

17. $y=2 \sin \left(\dfrac{2 \pi}{3}(x+4)\right)+5$

$Screen Shot 2023-02-25 at 4.13.25 PM.png$

19. $y=-5 \cos \left(\dfrac{\pi x}{180}\right)+12$

$Screen Shot 2023-02-25 at 4.14.03 PM.png$

21.

a $f(x)=3 \sin \left(x+\dfrac{2 \pi}{3}\right)$

b $f(x)=3 \cos \left(x+\dfrac{\pi}{6}\right)$

23.

a $f(x)=2 \sin \left(2\left(x-\dfrac{\pi}{4}\right)\right)$

b $f(x)=-2 \cos (2 x)$

25.

a $f(x)=4 \sin \left[\dfrac{1}{4}\left(x-\dfrac{7 \pi}{3}\right)\right]$

b $f(x)=-4 \cos \left[\dfrac{1}{4}\left(x-\dfrac{\pi}{3}\right)\right]$

27.

a midline $T=35.35$ , period 12 , amplitude 36.95

b $T(m)=-36.95 \cos \left(\dfrac{\pi}{6} m\right)+35.35$

c $Screen Shot 2023-02-25 at 4.19.48 PM.png$

29.

a midline $h=1.4$ , period $\frac{2 \pi}{0.51} \approx 12.32$ , amplitude 1.4

b $Screen Shot 2023-02-25 at 4.20.42 PM.png$

c high 11:10 am, low 5:19 pm

31.

a amplitude 3.2, period 2 , midline $y=2$

b $f(t)=2+3.2 \cos (\pi t)$

33.

a amplitude 5, period 1 , midline $y=0$

b $H(x)=5 \sin (2 \pi x)+5$

7.3 Solving Equations

Homework 7-3

1. $\dfrac{3 \pi}{8}, \dfrac{7 \pi}{8}, \dfrac{11 \pi}{8}, \dfrac{15 \pi}{8}$

3. $0, \dfrac{\pi}{2}, \pi, \dfrac{3 \pi}{2}, 2 \pi$

5. $\dfrac{2 \pi}{9}, \dfrac{4 \pi}{9}, \dfrac{8 \pi}{9}, \dfrac{10 \pi}{9}, \dfrac{14 \pi}{9}, \dfrac{16 \pi}{9}$

7. $\dfrac{\pi}{12}, \dfrac{5 \pi}{12}, \dfrac{13 \pi}{12}, \dfrac{17 \pi}{12}$

9. $\dfrac{\pi}{18}, \dfrac{7 \pi}{18}, \dfrac{13 \pi}{18}, \dfrac{19 \pi}{18}, \dfrac{25 \pi}{18}, \dfrac{31 \pi}{18}$

11. 0.491, 2.651, 3.632, 5.792

13. 0.540, 1.325, 2.110, 2.896, 3.681, 4.467, 5.252, 6.037

15. 1.114, 2.027, 3.209, 4.122, 5.303, 6.216

17. 0.702, 2.440, 3.843, 5.582

19. 0, 1, 2, 3, 4, 5, 6

21. $\dfrac{\pi}{6}, \dfrac{2 \pi}{3}, \dfrac{7 \pi}{6}, \dfrac{5 \pi}{3}$

23. $\dfrac{5 \pi}{12}, \dfrac{7 \pi}{12}, \dfrac{13 \pi}{12}, \dfrac{5 \pi}{4}, \dfrac{7 \pi}{4}, \dfrac{23 \pi}{12}$

25. $\dfrac{3\pi}{2}$

27. $\dfrac{7}{6}, \dfrac{11}{6}, \dfrac{19}{6}, \dfrac{23}{6}, \dfrac{31}{6}, \dfrac{35}{6}$

29. 1.14, 1.62, 3.23, 3.72, 5.24, 5.81

31. 0.44, 1.44, 2.44, 3.44, 4.44, 5.44

33. 0.01, 3.39, 6.01

35. 0.564, 1.182, 2.658, 3.276, 4.752, 5.371

37. 0.423, 2.977, 4.423

39. 1.165, 4.165

41. 2.251

43.

a $P(t)=4000 \cos \left(\dfrac{\pi}{6} t\right)+46,000$

b $t=\cos ^{-1}\left(\dfrac{-1}{4}\right) \cdot \dfrac{6}{\pi} \approx 3.48$ months (Dec) or $t=12-\cos ^{-1}\left(\dfrac{-1}{4}\right) \cdot \dfrac{6}{\pi} \approx 8.52$ months (June)

c $Screen Shot 2023-02-25 at 9.35.20 PM.png$

$P(t)$ is less than 45,000 between $A$ and $B$ .

45.

a $h(t)=11-10 \cos \left(\dfrac{\pi}{30} t\right)$

b $t=\cos (-0.7) \cdot \dfrac{30}{\pi} \approx 22.40 \mathrm{sec}$ or $t=60-\cos (-0.7) \cdot \dfrac{30}{\pi} \approx 37.60 \mathrm{sec}$

c $Screen Shot 2023-02-25 at 9.37.44 PM.png$

Delbert is above 18 m between $A$ and $B$ .

7.4 Chapter 7 Summary and Review

Review Problems

1. amp: 2, period: $\frac{2 \pi}{3}$ ; mid: $y=4$

3. amp: 2.5, period: 2; mid: $y=-2$

5. $Screen Shot 2023-02-25 at 9.44.02 PM.png$

7. $Screen Shot 2023-02-25 at 9.44.09 PM.png$

9. $y=3+2 \sin x$

11. $y=4-3 \sin \dfrac{x}{4}$

13.

a period: $4 \pi$ , shift: $\dfrac{\pi}{3}$ left

$x$	$\dfrac{x}{2}$	$\dfrac{x}{2} + \dfrac{\pi}{6}$	$\sin \left( \dfrac{x}{2} + \dfrac{\pi}{6} \right)$
$\dfrac{-2\pi}{3}$	$\dfrac{\pi}{3}$	$\dfrac{-\pi}{6}$	$\dfrac{-1}{2}$
$\dfrac{-\pi}{3}$	$\dfrac{-\pi}{6}$	0	0
0	0	$\dfrac{\pi}{6}$	$\dfrac{1}{2}$
$\dfrac{\pi}{6}$	$\dfrac{\pi}{12}$	$\dfrac{\pi}{4}$	$\dfrac{1}{\sqrt{2}}$
$\dfrac{\pi}{3}$	$\dfrac{\pi}{6}$	$\dfrac{\pi}{3}$	$\dfrac{\sqrt{3}}{2}$
$\dfrac{2\pi}{3}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	1
$\pi$	$\dfrac{\pi}{2}$	$\dfrac{2\pi}{3}$	$\dfrac{\sqrt{3}}{2}$

c $Screen Shot 2023-02-25 at 9.52.19 PM.png$

d $\dfrac{2\pi}{3}$

e $\dfrac{-\pi}{3}$

15.

a mid: $y=20$ , period: 0, amp: 5

b Fill in the table of values

$x$	$\dfrac{\pi}{30} x$	$\cos \left( \dfrac{\pi}{30} x \right)$	$20 - 5 \cos \left( \dfrac{\pi}{30} x \right)$
-5	$\dfrac{-\pi}{6}$	$\dfrac{\sqrt{3}}{2}$	$20 - \dfrac{\sqrt{3}}{2}$
0	0	1	15
5	$\dfrac{\pi}{6}$	$\dfrac{\sqrt{3}}{2}$	$20 - \dfrac{\sqrt{3}}{2}$
10	$\dfrac{\pi}{3}$	$\dfrac{1}{2}$	17.5
15	$\dfrac{\pi}{2}$	0	20
50	$\pi$	-1	25

c $Screen Shot 2023-02-25 at 9.58.43 PM.png$

d 30

e 15, 45

17. $Screen Shot 2023-02-25 at 9.59.11 PM.png$

19.

a $Screen Shot 2023-02-25 at 9.59.50 PM.png$

b 0.57, 3.07, 3.71

21. $y=85.5-19.5 \cos \dfrac{\pi}{6} t$

23.

a amp: 3, period: 12, midline: $y = 15$

b $y=15-3 \cos \dfrac{\pi}{6} t$

25. $\dfrac{7 \pi}{12}, \dfrac{11 \pi}{12}, \dfrac{19 \pi}{12}, \dfrac{23 \pi}{12}$

27. $0, \dfrac{\pi}{4}, \dfrac{\pi}{2}, \dfrac{3 \pi}{4}, \pi, \dfrac{5 \pi}{4}, \dfrac{7 \pi}{4}, 2 \pi$

29. 0.066, 1.113, 2.160, 3.207, 4.255, 5.302

31. 1.150, 1.991, 4.292, 5.133

33. $\dfrac{\pi}{24}, \dfrac{5 \pi}{24}, \dfrac{25 \pi}{24}, \dfrac{29 \pi}{24}$

35. No Solution

37. 0.375, 1.422, 2.470, 3.517, 4.564, 5.611

39. 2.120, 4.880

7.1 Transformations of Graphs

Homework 7-1

7.2 The General Sinusoidal Function

Homework 7-2

7.3 Solving Equations

Homework 7-3

7.4 Chapter 7 Summary and Review

Review Problems

Support Center

How can we help?