11.8: Vectors
- Page ID
- 122988
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)9.1 Geometric Form
Homework 9-1
1. 
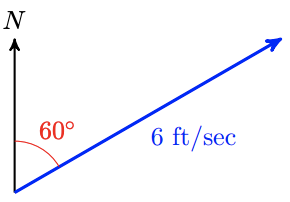
3. 
5. 
7. A and E
9. H and K
11. 
13. 
15. 
17. 
19. 
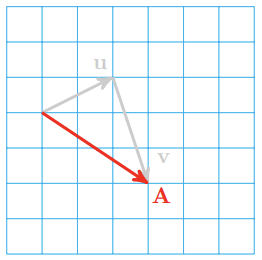\(\|\mathbf{A}\|=\sqrt{13}, \theta=-33.7^{\circ}\)
21. 
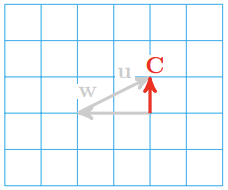\(\|\mathbf{C}\|=1, \quad \theta=90^{\circ}\)
23. 
\(\| \mathbf{E} \| = 5, \quad \theta = 90^{\circ}\)
25. 
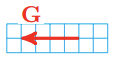\(\| \mathbf{G} = 4, \quad \theta = 180^{\circ}\)
27. \(\|\mathbf{v}\|=13, \quad \theta=-67.38^{\circ}\)
29. \(\|\mathbf{v}\|=\sqrt{85} \approx 9.22, \theta=229.4^{\circ}\)
31. 
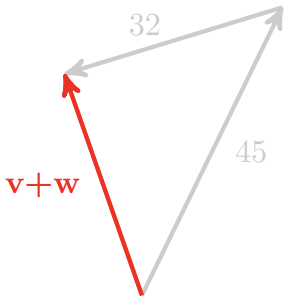\(\| v + w\| = 32.9, \quad \theta = 109.3^{\circ}\)
33. 
\(\|\mathbf{v}+\mathbf{w}\|=11.4, \theta=162.4^{\circ}\)
35. 
\(4.47 \mathrm{mi}, 23.4^{\circ}\) east of north
37. 
\(129.4 \mathrm{mph}, 85.4^{\circ}\) west of north
39.
a \(v_x=10, v_y=10 \sqrt{3}, w_x=5 \sqrt{2}, w_y=-5 \sqrt{2}\)
b \(19.9 \mathrm{mph}, 59^{\circ}\) east of north
41.
a \(v_x \approx-1.23, v_y \approx 3.38, w_x \approx-0.32, w_y \approx-2.23\)
b \(1.9 \mathrm{~km}, 54.5^{\circ}\) west of north
43. 
45. 
47. 
49. 
51. \(u_x=2, u_y=1, v_x=1, v_y=-3, A_x=1, A_y=4 ; A_x=u_x-v_x, A_y=u_y-v_y\)
9.2 Coordinate Form
Homework 9-2
1. \(\mathbf{u}=3 \mathbf{i}+2 \mathbf{j}\)
a \(\sqrt{13}\)
b \(6 \mathbf{i}+4 \mathbf{j}\)
c \(2 \sqrt{13}\)
3. \(\mathbf{w}=6 \mathbf{i}-3 \mathbf{j}\)
a \(3 \sqrt{5}\)
b \(-6 \mathbf{i}+3 \mathbf{j}\)
c \(3 \sqrt{5}\)
5.
a \(\mathbf{u}+\mathbf{v}=-2 \mathbf{i}+5 \mathbf{j}\) and \(\|\mathbf{u}+\mathbf{v}\|=\sqrt{29}\)
b \(\|\mathbf{u}\|+\|\mathbf{v}\| \geq\|\mathbf{u}+\mathbf{v}\|\)
7.
a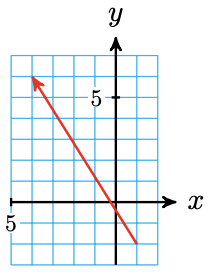 
\(-5 \mathbf{i}+8 \mathbf{j}\)
b \(\|\mathbf{v}\|=\sqrt{89}, \quad \theta=122^{\circ}\)
9.
a 
\(-2 \mathbf{i}-\mathbf{j}\)
b \(\|\mathbf{v}\|=\sqrt{5}, \quad \theta=206.6^{\circ}\)
11.
a \(18 \mathbf{i}+12 \mathbf{j}\)
b \(\|\mathbf{v}\|=6 \sqrt{13}, \quad \theta=33.7^{\circ}\)
13. \(\|\mathbf{v}\|=6 \sqrt{2}, \quad \theta=135^{\circ}\)
15. \(\|\mathbf{w}\|=14, \quad \theta=-30^{\circ}\)
17. \(\|\mathbf{q}\|=4 \sqrt{745}, \quad \theta=61.56^{\circ}\)
19. \(\mathbf{v}=3 \sqrt{2} \mathbf{i}-3 \sqrt{2} \mathbf{j}\)
21. \(\mathbf{v} \approx 6.629 \mathbf{i}+4.995 \mathbf{j}\)
23. \(\mathbf{i} - 2\mathbf{j}\)
25. \(-4 \mathbf{i} + 4 \mathbf{j}\)
27. \(12 \mathbf{i}+3 \mathbf{j}\)
29. \(2.8 \mathbf{i}+1.9 \mathbf{j}\)
31. \(-3 \mathbf{i}+7 \mathbf{j}\)
33. \(-8 \mathbf{i}-20 \mathbf{j}\)
35. \(14 \mathbf{i}-9 \mathbf{j}\)
37. \(-9 \mathbf{i}+23 \mathbf{j}\)
39. \(\dfrac{-12}{13} \mathbf{i}+\dfrac{5}{13} \mathbf{j}\)
41. \(\dfrac{1}{\sqrt{2}} \mathbf{i}-\dfrac{1}{\sqrt{2}} \mathbf{j}\)
43. \(24 \mathbf{i}+45 \mathbf{j}\)
45. \(\dfrac{-12}{\sqrt{10}} \mathbf{i}+\dfrac{4}{\sqrt{10}} \mathbf{j}\)
47.
a 
b \(\mathbf{u}=2.393 \mathbf{i}+1.016 \mathbf{j}, \quad \mathbf{v}=-4.242 \mathbf{i}-3.956 \mathbf{j}\)
c \(-1.849 \mathbf{i}-2.940 \mathbf{j}\)
49.
a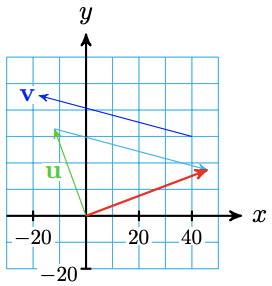 
b \(\mathbf{u}=-11.97 \mathbf{i}+32.889 \mathbf{j}, \quad \mathbf{v}=-57.955 \mathbf{i}+15.529 \mathbf{j}\)
c \(45.98 \mathbf{i}+17.36 \mathbf{j}\)
51.
a 
b \(1700 \mathrm{~m}, 28.1^{\circ}\) east of south
53.
a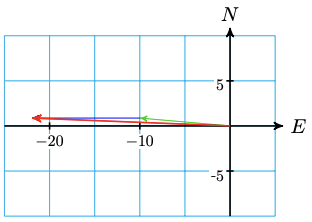 
b \(21.98 \mathrm{~km}, 2.27^{\circ}\) north of west
55.
a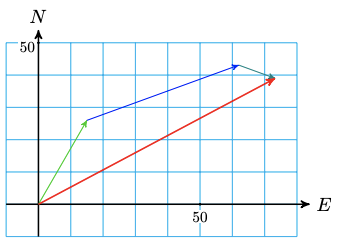 
b \(83 \mathrm{mi}, 62^{\circ}\) east of north
57.
a \(-4 \mathbf{i}-5 \mathbf{j}\)
b \(4 \mathbf{i}+5 \mathbf{j}\)
59.
a \(\mathbf{i}-3 \mathbf{j}\)
b \(-\mathbf{i}+3 \mathbf{j}\)
61.
a \(\|\mathbf{v}\|=10,2\|\mathbf{v}\|=20=2 \cdot 10\)
b \(\|k \mathbf{v}\|=\sqrt{(k a)^2+(k b)^2}=k \sqrt{a^2+b^2}\)
9.3 The Dot Product
Homework 9-3
1. \(\dfrac{33}{\sqrt{13}}\)
3. \(\dfrac{-1}{\sqrt{2}}\)
5. \(-2\sqrt{5}\)
7.
a \(\mathbf{w}=\left(\dfrac{56}{13} \mathbf{i}+\dfrac{84}{13} \mathbf{j}\right)+\left(\dfrac{48}{13} \mathbf{i}-\dfrac{32}{13} \mathbf{j}\right)\)
b 
9.
a \(\mathbf{w}=(4 \mathbf{i}-4 \mathbf{j})+(2 \mathbf{i}+2 \mathbf{j})\)
b 
11. 22
13. 0
15. 12
17. -318.2
19. not orthogonal
21. orthogonal
23. \(4.4^{\circ}\)
25. \(97.1^{\circ}\)
27. 8
29. -10
31. -21
33. \(42 \mathbf{i}-28 \mathbf{j}\)
35. 4
37. 38.57 lbs
39. 1289 lbs
41.
a \(\dfrac{1}{\sqrt{2}} \mathbf{i}+\dfrac{1}{\sqrt{2}} \mathbf{j}\) and \(\dfrac{-1}{\sqrt{2}} \mathbf{i}+\dfrac{1}{\sqrt{2}} \mathbf{j}\)
b \(\mathbf{u} \cdot \mathbf{v}=0\)
c \(\dfrac{11}{\sqrt{2}}\) and \(\dfrac{5}{\sqrt{2}}\)
d 
43. \(\mathbf{v} \cdot \mathbf{v}=c^2+d^2\)
45. \(k \mathbf{u} \cdot \mathbf{v}=k a c+k b d=k(a c+b d)=(a k c+b k d)\)
47.
\begin{aligned}
(\mathbf{u}-\mathbf{v}) \cdot(\mathbf{u}+\mathbf{v}) & =(a-c)(a+c)+(b-d)(b+d) \\
& =\left(a^2+b^2\right)-\left(c^2+d^2\right)
\end{aligned}
49. \(\dfrac{a \cdot 1+b \cdot 0}{1}=a \text { and } \dfrac{a \cdot 0+b \cdot 1}{1}=b\)
51.
a Both \(\mathbf{i} \cdot \mathbf{i}=1\) and \(\mathbf{j} \cdot \mathbf{j}=1\) because \(1 \cdot 1 \cos 0=1 ; \mathbf{i} \cdot \mathbf{j}=1 \cdot 1 \cos 90^{\circ}=0\)
b \((a \mathbf{i}+b \mathbf{j}) \cdot(c \mathbf{i}+d \mathbf{j})=a c(1)+a d(0)+b c(0)+b d(1)=a c+b d\)
53.
a \(\|\mathbf{u}-\mathbf{v}\|^2=\mathbf{u} \cdot \mathbf{u}-2 \mathbf{u} \cdot \mathbf{v}+\mathbf{v} \cdot \mathbf{v}=\|\mathbf{u}\|^2+\|\mathbf{v}\|^2-2\|\mathbf{u}\|\|\mathbf{v}\| \cos \theta\)
b Let \(a=\|\mathbf{u}\|, b=\|\mathbf{v}\|, c=\|\mathbf{u}-\mathbf{v}\|\), and \(C=\theta\)
9.4 Chapter Summary and Review
Review Problems
1. 
\(v_N=8.45 \mathrm{mph}, v_E=-18.13 \mathrm{mph}\)
3. 
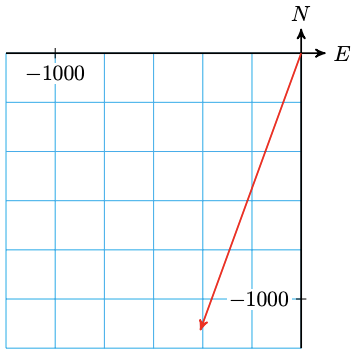\(v_N=-1127.63 \mathrm{lbs}, v_E=-410.42 \mathrm{lbs}\)
5. \(\|\mathbf{A}\|=10.9, \theta=236.3^{\circ}\)
7. \(\mathbf{i}-\sqrt{3} \mathbf{j}\)
9.
a 
\(15 \mathbf{i}+3 \mathbf{j}\)
b \(\|\mathbf{v}\|=15.3, \theta=11.3^{\circ}\)
11.
a 
\(2 \mathbf{i} - 6 \mathbf{j}\)
b \(\|\mathbf{v}\|=6.3 \mathrm{mi}, \theta=288.4^{\circ}\)
13.
a 
b \(7.64 \mathrm{~km}, \theta=30.31^{\circ}\)
15.
a 
b \(8.46 \mathrm{mi}, \theta=155.6^{\circ}\)
17.
a \(\mathbf{F}_1 = -200\mathbf{i}, \quad \mathbf{F}_2 = -60\sqrt{2}\mathbf{i} - 60\sqrt{2}\mathbf{j}, \quad \mathbf{F}_3 = 50\sqrt{3}\mathbf{i} + 50\mathbf{j}, \quad \mathbf{F}_4 = -125\mathbf{i} + 125\sqrt{3}\mathbf{j}\)
b \(-73.25 \mathbf{i}+181.65 \mathbf{j}\)
19. \(13 \mathbf{i}+5 \mathbf{j}\)
21. \(-7 \mathbf{i}-14 \mathbf{j}\)
23. \(\dfrac{2}{\sqrt{13}} \mathbf{i}+\dfrac{3}{\sqrt{13}} \mathbf{j}\)
25. \(\dfrac{-6}{\sqrt{29}} \mathrm{i}-\dfrac{15}{\sqrt{29}} \mathrm{j}\)
27. −3.45
29. −8.08
31. \(106.26^{\circ}\)