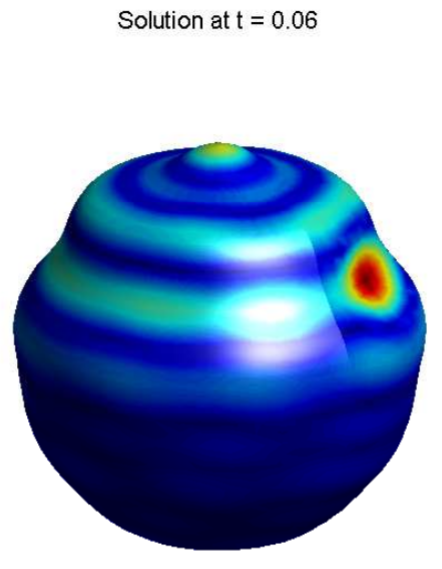
6.6: Spherically Symmetric Vibrations

Another application of spherical harmonics is a vibrating spherical membrane, such as a balloon. Just as for the two-dimensional membranes encountered earlier, we let \(u(\theta, \phi, t)\) represent the vibrations of the surface about a fixed radius obeying the wave equation, \(u_{t t}=c^{2} \nabla^{2} u\), and satisfying the initial conditions \[u(\theta, \phi, 0)=f(\theta, \phi), \quad u_{t}(\theta, \phi, 0)=g(\theta, \phi) .\nonumber \] In spherical coordinates, we have (for \(\rho=r=\) constant.) \[u_{t t}=\frac{c^{2}}{r^{2}}\left(\frac{1}{\sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial u}{\partial \theta}\right)+\frac{1}{\sin ^{2} \theta} \frac{\partial^{2} u}{\partial \phi^{2}}\right),\label{eq:1}\] where \(u=u(\theta, \phi, t)\).

Figure \(\PageIndex{1}\): A vibrating sphere of radius \(r\) with the initial conditions \[\begin{aligned} &u(\theta, \phi, 0)=f(\theta, \phi), \\ &u_{t}(\theta, \phi, 0)=g(\theta, \phi) . \end{aligned}\]

The boundary conditions are given by the periodic boundary conditions \[u(\theta, 0, t)=u(\theta, 2 \pi, t), \quad u_{\phi}(\theta, 0, t)=u_{\phi}(\theta, 2 \pi, t),\nonumber \] where \(0<t\), and \(0<\theta<\pi\), and that \(u=u(\theta, \phi, t)\) should remain bounded.

Noting that the wave equation takes the form \[u_{t t}=\frac{c^{2}}{r^{2}} L u, \quad \text { where } \quad L Y_{\ell m}=-\ell(\ell+1) Y_{\ell m}\nonumber \] for the spherical harmonics \(Y_{\ell m}(\theta, \phi)=P_{\ell}^{m}(\cos \theta) e^{i m \phi}\), then we can seek product solutions of the form \[u_{\ell m}(\theta, \phi, t)=T(t) Y_{\ell m}(\theta, \phi) .\nonumber \] Inserting this form into the wave equation in spherical coordinates, we find \[T^{\prime \prime} Y_{\ell m}=-\frac{c^{2}}{r^{2}} T(t) \ell(\ell+1) Y_{\ell m},\nonumber \] or \[T^{\prime \prime}+\ell(\ell+1) \frac{c^{2}}{r^{2}} T(t)\nonumber \] The solutions of this equation are easily found as \[T(t)=A \cos \omega_{\ell} t+B \sin \omega_{\ell} t, \quad \omega_{\ell}=\sqrt{\ell(\ell+1)} \frac{c}{r} .\nonumber \] Therefore, the product solutions are given by \[u_{\ell m}(\theta, \phi, t)=\left[A \cos \omega_{\ell} t+B \sin \omega_{\ell} t\right] Y_{\ell m}(\theta, \phi)\nonumber \] for \(\ell=0,1, \ldots, m=-\ell,-\ell+1, \ldots, \ell\).

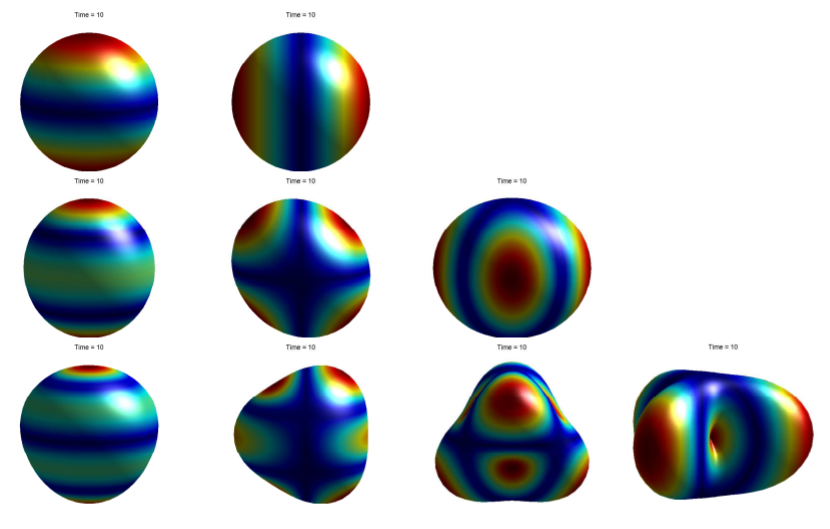
Figure \(\PageIndex{2}\): Modes for a vibrating spherical membrane: \[\begin{aligned}\text{Row }1:& (1,0), (1,1); \\ \text{Row }2:& (2,0), (2,1), (2,2); \\ \text{Row }3:& (3,0), (3,1), (3,2), (3,3).\end{aligned}\]

The general solution is found as \[u(\theta ,\phi ,t)=\sum\limits_{\ell=0}^\infty\sum\limits_{m=-\ell}^{\ell}[A_{\ell m}\cos\omega_{\ell}t+B_{\ell m}\sin\omega_{\ell}t]Y_{\ell m}(\theta ,\phi ).\nonumber\] An interesting problem is to consider hitting the balloon with a velocity impulse while at rest. An example of such a solution is shown in Figure \(\PageIndex{3}\). In this images several modes are excited after the impulse.

Figure \(\PageIndex{3}\): A moment captured from a simulation of a spherical membrane after hit with a velocity impulse.