6.7: Baking a Spherical Turkey

During one year as this course was being taught, an instructor returned from the American holiday of Thanksgiving, where it is customary to cook a turkey. Such a turkey is shown in Figure $\PageIndex{1}$. This reminded the instructor of a typical problem, such as in Weinberger, $(1995$, p. $92 .)$, where one is given a roast of a certain volume and one is asked to find the time it takes to cook one double the size. In this section, we explore a similar problem for cooking a turkey.

Figure $\PageIndex{1}$: A 12-lb turkey leaving the oven.

Often during this time of the year, November, articles appear with some scientific evidence as to how to gauge how long it takes to cook a turkey of a given weight. Inevitably it refers to the story, as told in today.slac.stanford.edu/a/2008/11-26.htm today.slac.stanford.edu/a/2008/1126.htm that Pief Panofsky, a former SLAC Director, was determined to find a nonlinear equation for determining cooking times instead of using the rule of thumb of 30 minutes per pound of turkey. He had arrived at the form,

$$t=\frac{W^{2 / 3}}{1.5}\nonumber$$

where $t$ is the cooking time and $W$ is the weight of the turkey in pounds. Nowadays, one can go to Wolframalpha.com and enter the question "how long should you cook a turkey" and get results based on a similar formula.

Before turning to the solution of the heat equation for a turkey, let’s consider a simpler problem.

Example $\PageIndex{1}$

If it takes 4 hours to cook a 10 pound turkey in a $350^{\circ}$ F oven, then how long would it take to cook a 20 pound turkey at the same conditions?

Solution

In all of our analysis, we will consider a spherical turkey. While the turkey in Figure $\PageIndex{1}$ is not quite spherical, we are free to approximate the turkey as such. If you prefer, we could imagine a spherical turkey like the one shown in Figure $\PageIndex{2}$.

This problem is one of scaling. Thinking of the turkey as being spherically symmetric, then the baking follows the heat equation in the form

$$u_{t}=\frac{k}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial u}{\partial r}\right) .\nonumber$$

We can rescale the variables from coordinates $(r, t)$ to $(\rho, \tau)$ as $r=\beta \rho$, and $t=\alpha \tau$. Then the derivatives transform as

$$\begin{align} &\frac{\partial}{\partial r}=\frac{\partial \rho}{\partial r} \frac{\partial}{\partial \rho}=\frac{1}{\beta} \frac{\partial}{\partial \rho},\nonumber \\ &\frac{\partial}{\partial t}=\frac{\partial \tau}{\partial t} \frac{\partial}{\partial \tau}=\frac{1}{\alpha} \frac{\partial}{\partial \tau} .\label{eq:1} \end{align}$$

Inserting these transformations into the heat equation, we have

$$u_{\tau}=\frac{\alpha}{\beta^{2}} \frac{k}{\rho^{2}} \frac{\partial}{\partial \rho}\left(\rho^{2} \frac{\partial u}{\partial \rho}\right)\nonumber$$

To keep conditions the same, then we need $\alpha=\beta^{2}$. So, the transformation that keeps the form of the heat equation the same, or makes it invariant, is $r=\beta \rho$, and $t=\beta^{2} \tau$. This is also known as a self-similarity transformation.

Figure $\PageIndex{2}$: The depiction of a spherical turkey.

So, if the radius increases by a factor of $\beta$, then the time to cook the turkey (reaching a given temperature, $u$ ), would increase by $\beta^{2}$. Returning to the problem, if the weight of the doubles, then the volume doubles, assuming that the density is held constant. However, the volume is proportional to $r^{3}$. So, $r$ increases by a factor of $2^{1 / 3}$. Therefore, the time increases by a factor of $2^{2 / 3} \approx 1.587$. This give the time for cooking a $20 \mathrm{lb}$ turkey as $t=4\left(2^{2 / 3}\right)=2^{8 / 3} \approx 6.35$ hours.

The previous example shows the power of using similarity transformations to get general information about solutions of differential equations. However, we have focussed on using the method of separation of variables for most of the book so far. We should be able to find a solution to the spherical turkey model using these methods as well. This will be shown in the next example.

Example $\PageIndex{2}$

Find the temperature, $T(\rho, t)$ inside a spherical turkey, initially at $40^{\circ}$, which is F placed in a $350^{\circ}$ F. Assume that the turkey is of constant density and that the surface of the turkey is maintained at the oven temperature. [We will also neglect convection and radaition processes inside the oven.]

Solution

The problem can be formulated as a heat equation problem for $T(\rho, t)$ :

$$\begin{align} T_{t} &=\frac{k}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial T}{\partial r}\right), \quad 0<\rho<a, t>0,\nonumber \\ T(a, t) &=350, \quad T(\rho, t) \text { finite at } \rho=0, \quad t>0,\nonumber \\ T(\rho, 0) &=40 .\label{eq:2} \end{align}$$

We note that the boundary condition is not homogeneous. However, we can fix that by introducing the auxiliary function (the difference between the turkey and oven temperatures) $u(\rho, t)=T(\rho, t)-T_{a}$, where $T_{a}=350$. Then, the problem to be solved becomes

$$\begin{align} u_{t} &=\frac{k}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial u}{\partial r}\right), \quad 0<\rho<a, t>0,\nonumber \\ u(a, t) &=0, \quad u(\rho, t) \quad \text { finite at } \rho=0, \quad t>0,\nonumber \\ u(\rho, 0) &=T_{a} i-T_{a}=-310,\label{eq:3} \end{align}$$

where $T_{i}=40$.

We can now employ the method of separation of variables. Let $u(\rho, t)=R(\rho) G(t)$. Inserting into the heat equation for $u$, we have

$$\frac{1}{k} \frac{G^{\prime}}{G}=\frac{1}{R}\left(R^{\prime \prime}+\frac{2}{\rho} R^{\prime}\right)=-\lambda .\nonumber$$

This give the two ordinary differential equations, the temporal equation,

$$G^{\prime}=-k \lambda G,\label{eq:4}$$

and the radial equation,

$$\rho R^{\prime \prime}+2 R^{\prime}+\lambda \rho R=0 .\label{eq:5}$$

The temporal equation is easy to solve,

$$G(t)=G_{0} e^{-\lambda k t} .\nonumber$$

However, the radial equation is slightly more difficult. But, making the substitution $R(\rho)=y(\rho) / \rho$, it is readily transformed into a simpler form:$^{1}$

$$y^{\prime \prime}+\lambda y=0\nonumber$$

The boundary conditions on $u(\rho, t)=R(\rho) G(t)$ transfer to $R(a)=0$ and $R(\rho)$ finite at the origin. In turn, this means that $y(a)=0$ and $y(\rho)$ has to vanish near the origin. If $y(\rho)$ does not vanish near the origin, then $R(\rho)$ is not finite as $\rho \rightarrow 0$.

So, we need to solve the boundary value problem

$$y^{\prime \prime}+\lambda y=0, \quad y(0)=0, \quad y(a)=0 .\nonumber$$

This gives the well-known set of eigenfunctions

$$y(\rho)=\sin \frac{n \pi \rho}{a}, \quad \lambda_{n}=\left(\frac{n \pi}{a}\right)^{2}, \quad n=1,2,3, \ldots .\nonumber$$

Therefore, we have found

$$R(\rho)=\frac{\sin \frac{n \pi \rho}{a}}{\rho}, \quad \lambda_{n}=\left(\frac{n \pi}{a}\right)^{2}, \quad n=1,2,3, \ldots .\nonumber$$

The general solution to the auxiliary problem is

$$u(\rho, t)=\sum_{n=1}^{\infty} A_{n} \frac{\sin \frac{n \pi \rho}{a}}{\rho} e^{-(n \pi / a)^{2} k t} .\nonumber$$

This gives the general solution for the temperature as

$$T(\rho, t)=T_{a}+\sum_{n=1}^{\infty} A_{n} \frac{\sin \frac{n \pi \rho}{a}}{\rho} e^{-(n \pi / a)^{2} k t} .\nonumber$$

All that remains is to find the solution satisfying the initial condition, $T(\rho,0=40$. Inserting $t=0$, we have

$$T_{i}-T_{a}=\sum_{n=1}^{\infty} A_{n} \frac{\sin \frac{n \pi \rho}{a}}{\rho}\nonumber$$

This is almost a Fourier sine series. Multiplying by $\rho$, we have

$$\left(T_{i}-T_{a}\right) \rho=\sum_{n=1}^{\infty} A_{n} \sin \frac{n \pi \rho}{a} .\nonumber$$

Now, we can solve for the coefficients,

$$\begin{align} A_{n} &=\frac{2}{a} \int_{0}^{a}\left(T_{i}-T_{a}\right) \rho \sin \frac{n \pi \rho}{a} d \rho\nonumber \\ &=\frac{2 a}{n \pi}\left(T_{i}-T_{a}\right)(-1)^{n+1} .\label{eq:6} \end{align}$$

This gives the final solution,

$$T(\rho, t)=T_{a}+\frac{2 a\left(T_{i}-T_{a}\right)}{\pi} \sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n} \frac{\sin \frac{n \pi \rho}{a}}{\rho} e^{-(n \pi / a)^{2} k t} .\nonumber$$

For generality, the ambient and initial temperature were left in terms of $T_{a}$ and $T_{i}$, respectively.

Note

The radial equation almost looks familiar when it is multiplied by $\rho$ :

$$\rho^{2} R^{\prime \prime}+2 \rho R^{\prime}+\lambda \rho^{2} R=0 .\nonumber$$

If it were not for the ’ 2 ’, it would be the zeroth order Bessel equation. This is actually the zeroth order spherical Bessel equation. In general, the spherical Bessel functions, $j_{n}(x)$ and $y_{n}(x)$, satisfy

$$x^{2} y^{\prime \prime}+2 x y^{\prime}+\left[x^{2}-n(n+1)\right] y=0 .\nonumber$$

So, the radial solution of the turkey problem is

$$R(\rho)=j_{n}(\sqrt{\lambda} \rho)=\frac{\sin \sqrt{\lambda} \rho}{\sqrt{\lambda} \rho} .\nonumber$$

We further note that

$$j_{n}(x)=\sqrt{\frac{\pi}{2 x}} J_{n+\frac{1}{2}}(x)\nonumber$$

It is interesting to use the above solution to compare roasting different turkeys. We take the same conditions as above. Let the radius of the spherical turkey be six inches. We will assume that such a turkey takes four hours to cook, i.e., reach a temperature of $180^{\circ}$ F. Plotting the solution with 400 terms, one finds that $k \approx 0.000089$. This gives a "baking time" of $t 1=239.63$. A plot of the temperature at the center point $(\rho=a / 2)$ of the bird is in Figure $\PageIndex{3}$.

Figure $\PageIndex{3}$: The temperature at the center of a turkey with radius $a=0.5 \mathrm{ft}$ and $k \approx 0.000089$.

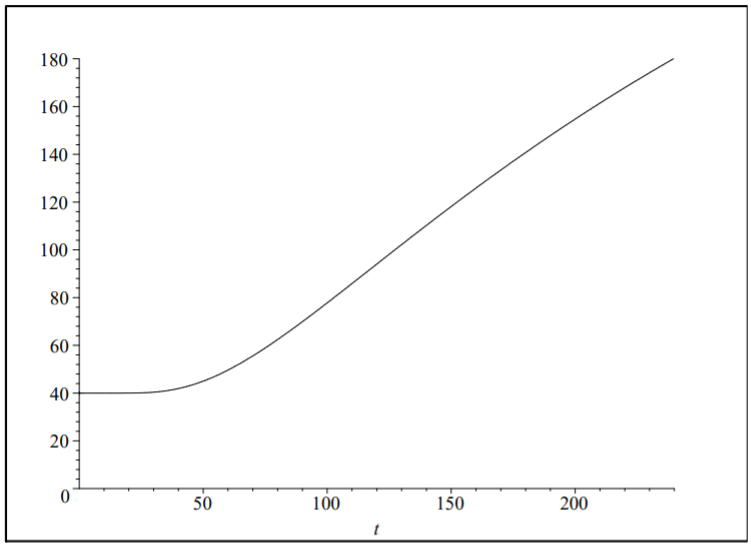
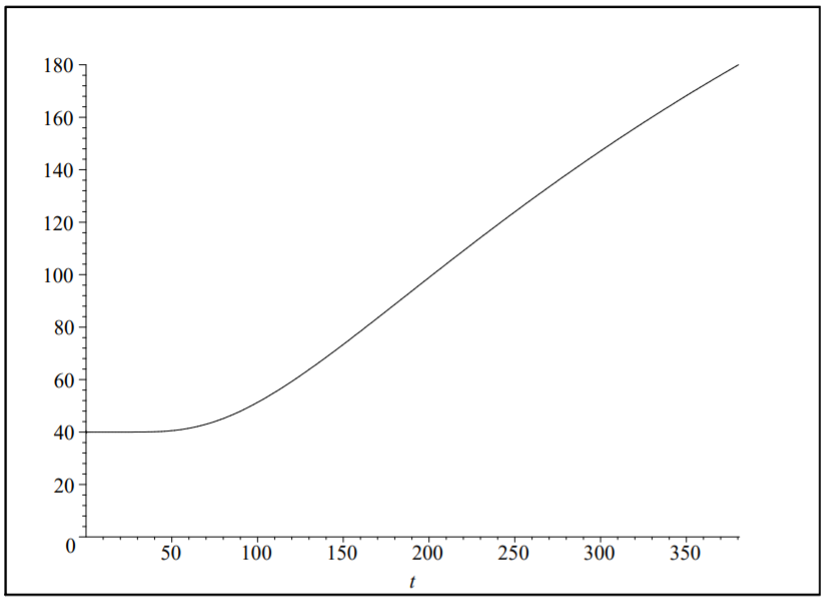
Using the same constants, but increasing the radius of a turkey to $a=$ $0.5\left(2^{1 / 3}\right) \mathrm{ft}$, we obtain the temperature plot in Figure $\PageIndex{4}$. This radius corresponds to doubling the volume of the turkey. Solving for the time at which the center temperature (at $\rho=a / 2$ ) reaches $180^{\circ} \mathrm{F}$, we obtained $t 2=380.38$. Comparing the two temperatures, we find the ratio (using the full computation of the solution in Maple)

$$\frac{t 2}{t 1}=\frac{380.3813709}{239.6252478} \approx 1.587401054 \text {. }\nonumber$$

The compares well to

$$2^{2 / 3} \approx 1.587401052 .\nonumber$$

Figure $\PageIndex{4}$: The temperature at the center of a turkey with radius $a=0.5(2^{1/3})\text{ ft}$ and $k\approx 0.000089$.

Of course, the temperature is not quite the center of the spherical turkey. The reader can work out the details for other locations. Perhaps other interesting models would be a spherical shell of turkey with a corse of bread stuffing. Or, one might consider an ellipsoidal geometry.