3.2: One-to-one and Onto Transformations
- Page ID
- 70196
- Understand the definitions of one-to-one and onto transformations.
- Recipes: verify whether a matrix transformation is one-to-one and/or onto.
- Pictures: examples of matrix transformations that are/are not one-to-one and/or onto.
- Vocabulary words: one-to-one, onto.
In this section, we discuss two of the most basic questions one can ask about a transformation: whether it is one-to-one and/or onto. For a matrix transformation, we translate these questions into the language of matrices.
One-to-one Transformations
A transformation \(T\colon\mathbb{R}^n \to\mathbb{R}^m \) is one-to-one if, for every vector \(b\) in \(\mathbb{R}^m \text{,}\) the equation \(T(x)=b\) has at most one solution \(x\) in \(\mathbb{R}^n \).
Another word for one-to-one is injective.
Here are some equivalent ways of saying that \(T\) is one-to-one:
- For every vector \(b\) in \(\mathbb{R}^m \text{,}\) the equation \(T(x) = b\) has zero or one solution \(x\) in \(\mathbb{R}^n \).
- Different inputs of \(T\) have different outputs.
- If \(T(u) = T(v)\) then \(u=v\).
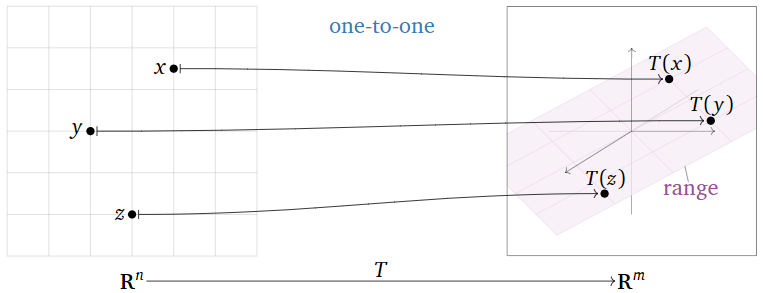
Figure \(\PageIndex{1}\)
Here are some equivalent ways of saying that \(T\) is not one-to-one:
- There exists some vector \(b\) in \(\mathbb{R}^m \) such that the equation \(T(x)=b\) has more than one solution \(x\) in \(\mathbb{R}^n \).
- There are two different inputs of \(T\) with the same output.
- There exist vectors \(u,v\) such that \(u\neq v\) but \(T(u)=T(v)\).
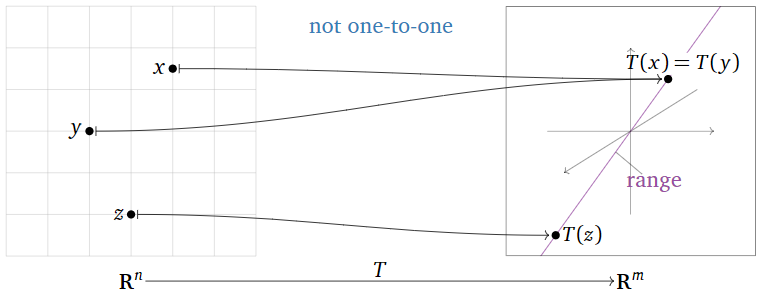
Figure \(\PageIndex{2}\)
The function \(\sin\colon \mathbb{R} \to\mathbb{R} \) is not one-to-one. Indeed, \(\sin(0) = \sin(\pi) = 0\text{,}\) so the inputs \(0\) and \(\pi\) have the same output \(0\). In fact, the equation \(\sin(x) = 0\) has infinitely many solutions \(\ldots,-2\pi,-\pi,0,\pi,2\pi,\ldots\).
The function \(\exp\colon \mathbb{R} \to\mathbb{R} \) defined by \(\exp(x) = e^x\) is one-to-one. Indeed, if \(T(x) = T(y)\text{,}\) then \(e^x = e^y\text{,}\) so \(\ln(e^x) = \ln(e^y)\text{,}\) and hence \(x = y\). The equation \(T(x) = C\) has one solution \(x = \ln(C)\) if \(C > 0\text{,}\) and it has zero solutions if \(C\leq 0\).
The function \(f\colon \mathbb{R} \to\mathbb{R} \) defined by \(f(x)=x^3\) is one-to-one. Indeed, if \(f(x) = f(y)\) then \(x^3 = y^3\text{;}\) taking cube roots gives \(x = y\). In other words, the only solution of \(f(x) = C\) is \(x=\sqrt[3]C\).
The function \(f\colon \mathbb{R} \to\mathbb{R} \) defined by \(f(x)=x^3-x\) is not one-to-one. Indeed, \(f(0) = f(1) = f(-1) = 0\text{,}\) so the inputs \(0,1,-1\) all have the same output \(0\). The solutions of the equation \(x^3 - x = 0\) are exactly the roots of \(f(x) = x(x-1)(x+1)\text{,}\) and this equation has three roots.
The function \(f\colon \mathbb{R} \to\mathbb{R} \) defined by \(f(x)=x^2\) is not one-to-one. Indeed, \(f(1) = 1 = f(-1)\text{,}\) so the inputs \(1\) and \(-1\) have the same outputs. The function \(g\colon \mathbb{R} \to\mathbb{R} \) defined by \(g(x)=|x|\) is not one-to-one for the same reason.
Suppose you are building a robot arm with three joints that can move its hand around a plane, as in Example 3.1.11 in Section 3.1.
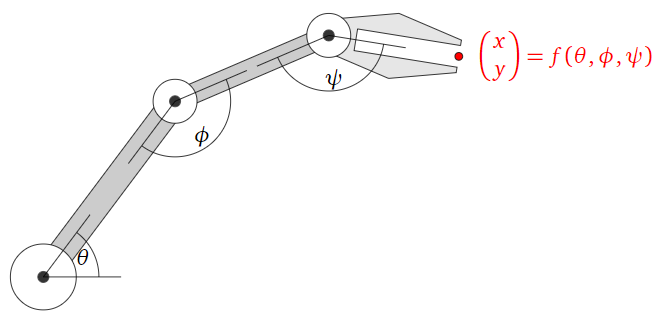
Figure \(\PageIndex{3}\)
Define a transformation \(f\colon\mathbb{R}^3 \to\mathbb{R}^2 \) as follows: \(f(\theta,\phi,\psi)\) is the \((x,y)\) position of the hand when the joints are rotated by angles \(\theta, \phi, \psi\text{,}\) respectively. Asking whether \(f\) is one-to-one is the same as asking whether there is more than one way to move the arm in order to reach your coffee cup. (There is.)
Let \(A\) be an \(m\times n\) matrix, and let \(T(x)=Ax\) be the associated matrix transformation. The following statements are equivalent:
- \(T\) is one-to-one.
- For every \(b\) in \(\mathbb{R}^m \text{,}\) the equation \(T(x)=b\) has at most one solution.
- For every \(b\) in \(\mathbb{R}^m \text{,}\) the equation \(Ax=b\) has a unique solution or is inconsistent.
- \(Ax=0\) has only the trivial solution.
- The columns of \(A\) are linearly independent.
- \(A\) has a pivot in every column.
- The range of \(T\) has dimension \(n\).
- Proof
-
Statements 1, 2, and 3 are translations of each other. The equivalence of 3 and 4 follows from key observation 2.4.3 in Section 2.4: if \(Ax=0\) has only one solution, then \(Ax=b\) has only one solution as well, or it is inconsistent. The equivalence of 4, 5, and 6 is a consequence of Recipe: Checking Linear Independence in Section 2.5, and the equivalence of 6 and 7 follows from the fact that the rank of a matrix is equal to the number of columns with pivots.
Recall that equivalent means that, for a given matrix, either all of the statements are true simultaneously, or they are all false.
Let \(A\) be the matrix
\[A=\left(\begin{array}{cc}1&0\\0&1\\1&0\end{array}\right),\nonumber\]
and define \(T\colon\mathbb{R}^2 \to\mathbb{R}^3 \) by \(T(x) = Ax\). Is \(T\) one-to-one?
Solution
The reduced row echelon form of \(A\) is
\[\left(\begin{array}{cc}1&0\\0&1\\0&0\end{array}\right).\nonumber\]
Hence \(A\) has a pivot in every column, so \(T\) is one-to-one.
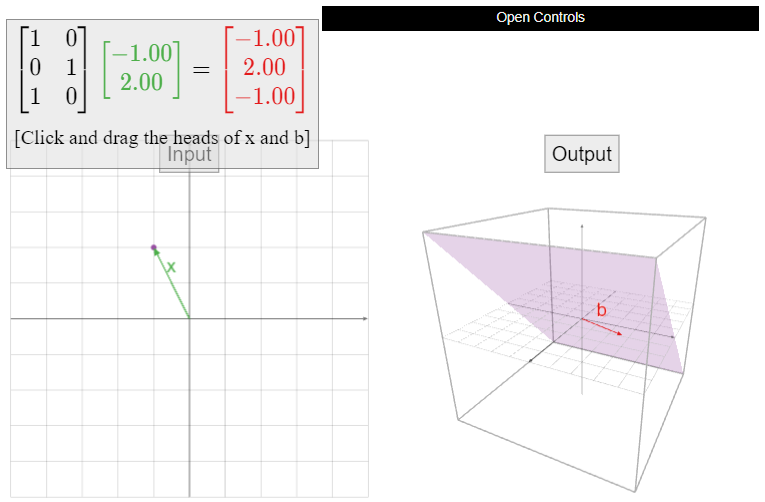
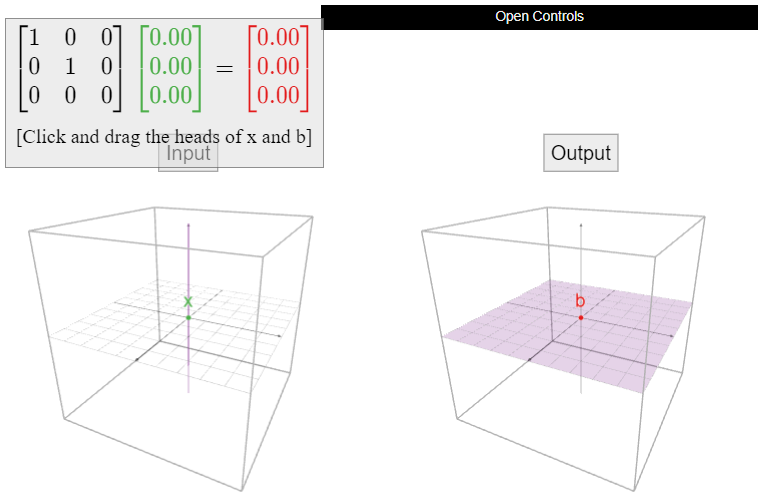
Let
\[A=\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&0\end{array}\right),\nonumber\]
and define \(T\colon\mathbb{R}^3 \to\mathbb{R}^3 \) by \(T(x) = Ax\). Is \(T\) one-to-one? If not, find two different vectors \(u,v\) such that \(T(u)=T(v)\).
Solution
The matrix \(A\) is already in reduced row echelon form. It does not have a pivot in every column, so \(T\) is not one-to-one. Therefore, we know from the Theorem \(\PageIndex{1}\) that \(Ax=0\) has nontrivial solutions. If \(v\) is a nontrivial (i.e., nonzero) solution of \(Av = 0\text{,}\) then \(T(v) = Av = 0 = A0 = T(0)\text{,}\) so \(0\) and \(v\) are different vectors with the same output. For instance,
\[T\left(\begin{array}{c}0\\0\\1\end{array}\right)=\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&0\end{array}\right)\:\left(\begin{array}{c}0\\0\\1\end{array}\right)=0=T\left(\begin{array}{c}0\\0\\0\end{array}\right).\nonumber\]
Geometrically, \(T\) is projection onto the \(xy\)-plane. Any two vectors that lie on the same vertical line will have the same projection. For \(b\) on the \(xy\)-plane, the solution set of \(T(x) = b\) is the entire vertical line containing \(b\). In particular, \(T(x) = b\) has infinitely many solutions.
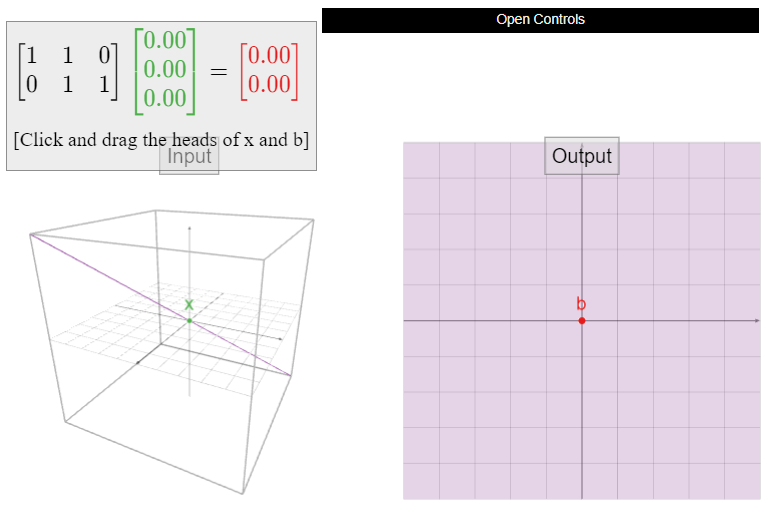
Let \(A\) be the matrix
\[A=\left(\begin{array}{ccc}1&1&0\\0&1&1\end{array}\right),\nonumber\]
and define \(T\colon\mathbb{R}^3 \to\mathbb{R}^2 \) by \(T(x) = Ax\). Is \(T\) one-to-one? If not, find two different vectors \(u,v\) such that \(T(u)=T(v)\).
Solution
The reduced row echelon form of \(A\) is
\[\left(\begin{array}{ccc}1&0&-1\\0&1&1\end{array}\right).\nonumber\]
There is not a pivot in every column, so \(T\) is not one-to-one. Therefore, we know from Theorem \(\PageIndex{1}\) that \(Ax=0\) has nontrivial solutions. If \(v\) is a nontrivial (i.e., nonzero) solution of \(Av = 0\text{,}\) then \(T(v) = Av = 0 = A0 = T(0)\text{,}\) so \(0\) and \(v\) are different vectors with the same output. In order to find a nontrivial solution, we find the parametric form of the solutions of \(Ax=0\) using the reduced matrix above:
\[\left\{\begin{array}{rrrrrrr}x &{}&{}& -& z &=& 0\\ {}&{}& y& + &z &=& 0\end{array}\right.\quad\implies\quad\left\{\begin{array}{rrr}x&=&z \\ y&=&-z\end{array}\right.\nonumber\]
The free variable is \(z\). Taking \(z=1\) gives the nontrivial solution
\[T\left(\begin{array}{c}1\\-1\\1\end{array}\right)=\left(\begin{array}{ccc}1&1&0\\0&1&1\end{array}\right)\:\left(\begin{array}{c}1\\-1\\1\end{array}\right)=0=T\left(\begin{array}{c}0\\0\\0\end{array}\right).\nonumber\]
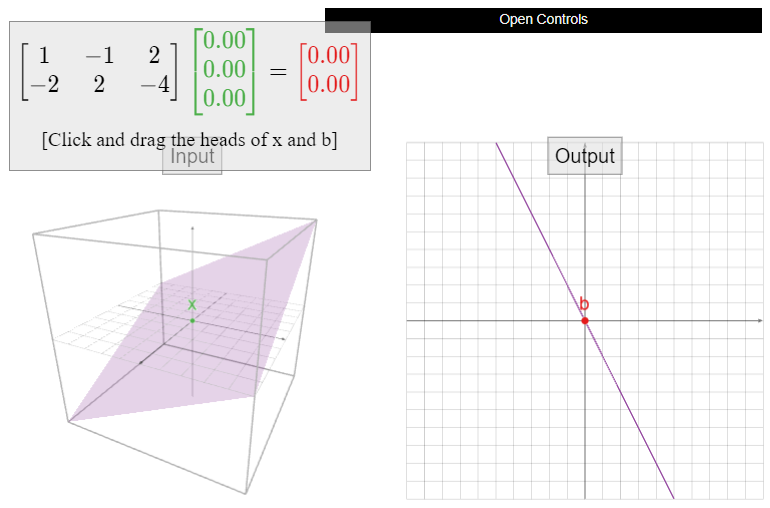
Let
\[A=\left(\begin{array}{ccc}1&-1&2\\-2&2&-4\end{array}\right),\nonumber\]
and define \(T\colon\mathbb{R}^3 \to\mathbb{R}^2 \) by \(T(x) = Ax\). Is \(T\) one-to-one? If not, find two different vectors \(u,v\) such that \(T(u)=T(v)\).
Solution
The reduced row echelon form of \(A\) is
\[\left(\begin{array}{ccc}1&-1&2\\0&0&0\end{array}\right).\nonumber\]
There is not a pivot in every column, so \(T\) is not one-to-one. Therefore, we know from Theorem \(\PageIndex{1}\) that \(Ax=0\) has nontrivial solutions. If \(v\) is a nontrivial (i.e., nonzero) solution of \(Av = 0\text{,}\) then \(T(v) = Av = 0 = A0 = T(0)\text{,}\) so \(0\) and \(v\) are different vectors with the same output. In order to find a nontrivial solution, we find the parametric form of the solutions of \(Ax=0\) using the reduced matrix above:
\[ x - y + 2z = 0 \quad\implies\quad x = y - 2z. \nonumber \]
The free variables are \(y\) and \(z\). Taking \(y=1\) and \(z=0\) gives the nontrivial solution
\[T\left(\begin{array}{c}1\\1\\0\end{array}\right)=\left(\begin{array}{ccc}1&-1&2\\-2&2&-4\end{array}\right)\:\left(\begin{array}{c}1\\1\\0\end{array}\right)=0=T\left(\begin{array}{c}0\\0\\0\end{array}\right).\nonumber\]
The previous three examples can be summarized as follows. Suppose that \(T(x)=Ax\) is a matrix transformation that is not one-to-one. By Theorem \(\PageIndex{1}\), there is a nontrivial solution of \(Ax=0\). This means that the null space of \(A\) is not the zero space. All of the vectors in the null space are solutions to \(T(x)=0\). If you compute a nonzero vector \(v\) in the null space (by row reducing and finding the parametric form of the solution set of \(Ax=0\text{,}\) for instance), then \(v\) and \(0\) both have the same output: \(T(v) = Av = 0 = T(0).\)
If \(T\colon\mathbb{R}^n \to\mathbb{R}^m \) is a one-to-one matrix transformation, what can we say about the relative sizes of \(n\) and \(m\text{?}\)
The matrix associated to \(T\) has \(n\) columns and \(m\) rows. Each row and each column can only contain one pivot, so in order for \(A\) to have a pivot in every column, it must have at least as many rows as columns: \(n\leq m\).
This says that, for instance, \(\mathbb{R}^3 \) is “too big” to admit a one-to-one linear transformation into \(\mathbb{R}^2 \).
Note that there exist tall matrices that are not one-to-one: for example,
\[\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&0\\0&0&0\end{array}\right)\nonumber\]
does not have a pivot in every column.
Onto Transformations
A transformation \(T\colon\mathbb{R}^n \to\mathbb{R}^m \) is onto if, for every vector \(b\) in \(\mathbb{R}^m \text{,}\) the equation \(T(x)=b\) has at least one solution \(x\) in \(\mathbb{R}^n \).
Another word for onto is surjective.
Here are some equivalent ways of saying that \(T\) is onto:
- The range of \(T\) is equal to the codomain of \(T\).
- Every vector in the codomain is the output of some input vector.
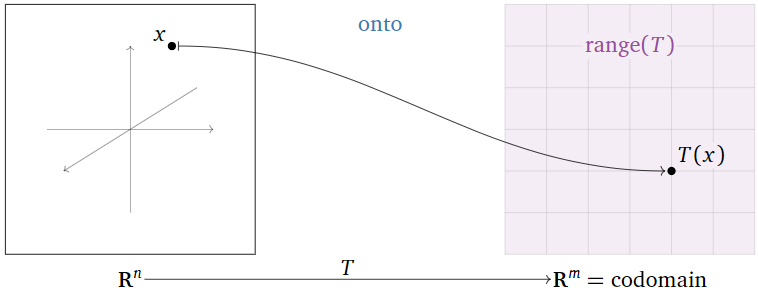
Figure \(\PageIndex{8}\)
Here are some equivalent ways of saying that \(T\) is not onto:
- The range of \(T\) is smaller than the codomain of \(T\).
- There exists a vector \(b\) in \(\mathbb{R}^m \) such that the equation \(T(x)=b\) does not have a solution.
- There is a vector in the codomain that is not the output of any input vector.
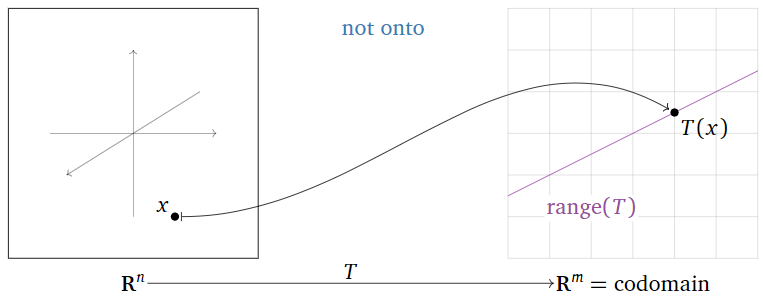
Figure \(\PageIndex{9}\)
The function \(\sin\colon \mathbb{R} \to\mathbb{R} \) is not onto. Indeed, taking \(b=2\text{,}\) the equation \(\sin(x)=2\) has no solution. The range of \(\sin\) is the closed interval \([-1,1]\text{,}\) which is smaller than the codomain \(\mathbb{R}\).
The function \(\exp\colon \mathbb{R} \to\mathbb{R} \) defined by \(\exp(x) = e^x\) is not onto. Indeed, taking \(b=-1\text{,}\) the equation \(\exp(x) = e^x = -1\) has no solution. The range of \(\exp\) is the set \((0,\infty)\) of all positive real numbers.
The function \(f\colon \mathbb{R} \to\mathbb{R} \) defined by \(f(x)=x^3\) is onto. Indeed, the equation \(f(x) = x^3 = b\) always has the solution \(x = \sqrt[3]b\).
The function \(f\colon \mathbb{R} \to\mathbb{R} \) defined by \(f(x)=x^3-x\) is onto. Indeed, the solutions of the equation \(f(x) = x^3 - x = b\) are the roots of the polynomial \(x^3 - x - b\text{;}\) as this is a cubic polynomial, it has at least one real root.
The robot arm transformation of Example \(\PageIndex{2}\) is not onto. The robot cannot reach objects that are very far away.
Let \(A\) be an \(m\times n\) matrix, and let \(T(x)=Ax\) be the associated matrix transformation. The following statements are equivalent:
- \(T\) is onto.
- \(T(x)=b\) has at least one solution for every \(b\) in \(\mathbb{R}^m \).
- \(Ax=b\) is consistent for every \(b\) in \(\mathbb{R}^m \).
- The columns of \(A\) span \(\mathbb{R}^m \).
- \(A\) has a pivot in every row.
- The range of \(T\) has dimension \(m\).
- Proof
-
Statements 1, 2, and 3 are translations of each other. The equivalence of 3, 4, 5, and 6 follows from Theorem 2.3.1 in Section 2.3.
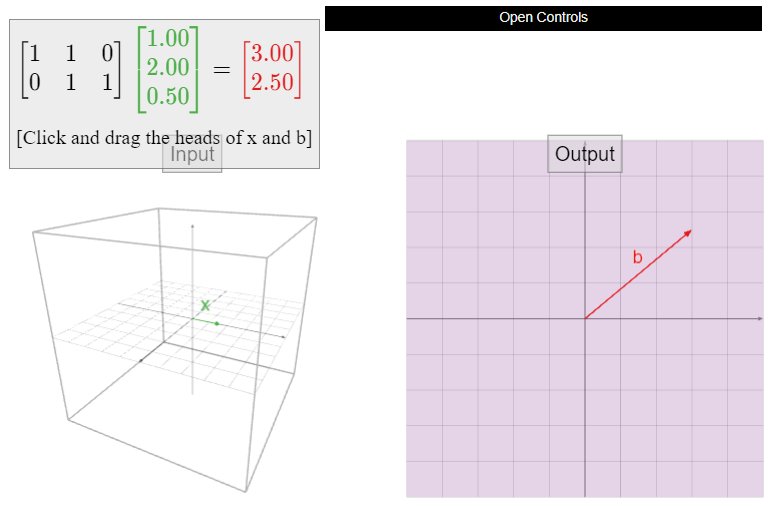
Let \(A\) be the matrix
\[A=\left(\begin{array}{ccc}1&1&0\\0&1&1\end{array}\right),\nonumber\]
and define \(T\colon\mathbb{R}^3 \to\mathbb{R}^2 \) by \(T(x) = Ax\). Is \(T\) onto?
Solution
The reduced row echelon form of \(A\) is
\[\left(\begin{array}{ccc}1&0&-1\\0&1&1\end{array}\right).\nonumber\]
Hence \(A\) has a pivot in every row, so \(T\) is onto.
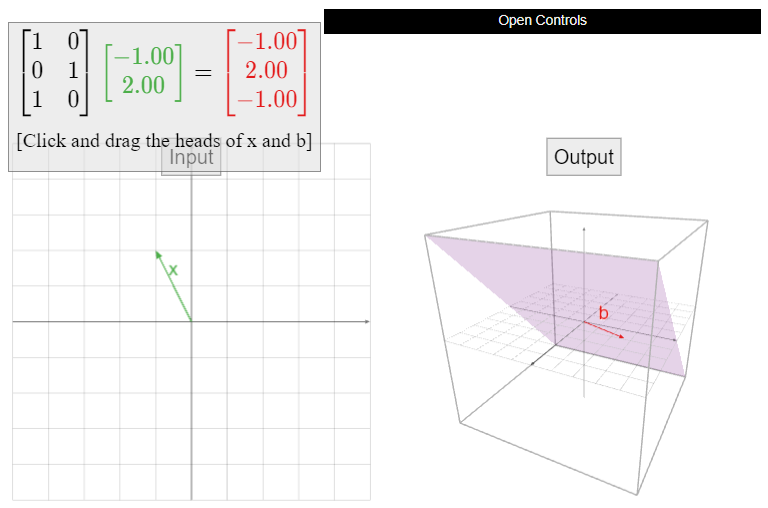
Let \(A\) be the matrix
\[A=\left(\begin{array}{cc}1&0\\0&1\\1&0\end{array}\right),\nonumber\]
and define \(T\colon\mathbb{R}^2 \to\mathbb{R}^3 \) by \(T(x) = Ax\). Is \(T\) onto? If not, find a vector \(b\) in \(\mathbb{R}^3 \) such that \(T(x)=b\) has no solution.
Solution
The reduced row echelon form of \(A\) is
\[\left(\begin{array}{cc}1&0\\0&1\\0&0\end{array}\right).\nonumber\]
Hence \(A\) does not have a pivot in every row, so \(T\) is not onto. In fact, since
\[T\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{cc}1&0\\0&1\\1&0\end{array}\right)\:\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}x\\y\\x\end{array}\right),\nonumber\]
we see that for every output vector of \(T\text{,}\) the third entry is equal to the first. Therefore,
\[ b=(1,2,3) \nonumber \]
is not in the range of \(T\).
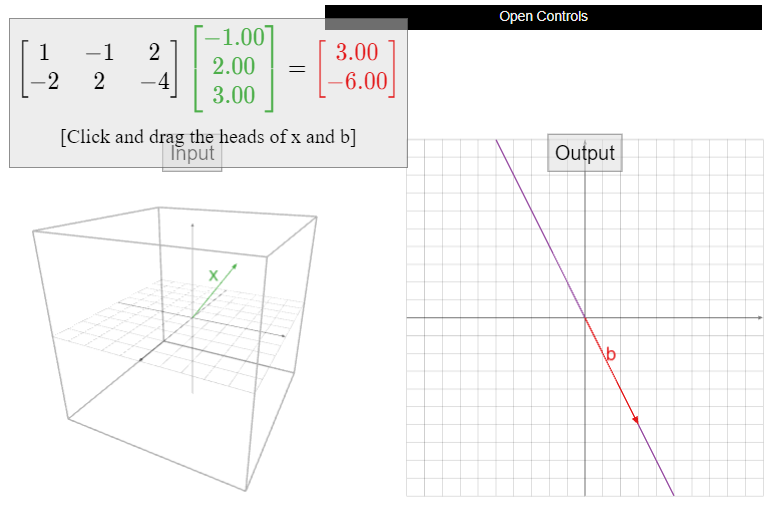
Let
\[A=\left(\begin{array}{ccc}1&-1&2\\-2&2&4\end{array}\right),\nonumber\]
and define \(T\colon\mathbb{R}^3 \to\mathbb{R}^2 \) by \(T(x) = Ax\). Is \(T\) onto? If not, find a vector \(b\) in \(\mathbb{R}^2 \) such that \(T(x)=b\) has no solution.
Solution
The reduced row echelon form of \(A\) is
\[\left(\begin{array}{ccc}1&-1&2\\0&0&0\end{array}\right).\nonumber\]
There is not a pivot in every row, so \(T\) is not onto. The range of \(T\) is the column space of \(A\text{,}\) which is equal to
\[\text{Span}\left\{\left(\begin{array}{c}1\\-2\end{array}\right),\:\left(\begin{array}{c}-1\\2\end{array}\right),\:\left(\begin{array}{c}2\\-4\end{array}\right)\right\}=\text{Span}\left\{\left(\begin{array}{c}1\\-2\end{array}\right)\right\},\nonumber\]
since all three columns of \(A\) are collinear. Therefore, any vector not on the line through \(1\choose-2\) is not in the range of \(T\). For instance, if \(b={1\choose 1}\) then \(T(x)=b\) has no solution.
The previous two examples illustrate the following observation. Suppose that \(T(x)=Ax\) is a matrix transformation that is not onto. This means that \(\text{range}(T) = \text{Col}(A)\) is a subspace of \(\mathbb{R}^m \) of dimension less than \(m\text{:}\) perhaps it is a line in the plane, or a line in \(3\)-space, or a plane in \(3\)-space, etc. Whatever the case, the range of \(T\) is very small compared to the codomain. To find a vector not in the range of \(T\text{,}\) choose a random nonzero vector \(b\) in \(\mathbb{R}^m \text{;}\) you have to be extremely unlucky to choose a vector that is in the range of \(T\). Of course, to check whether a given vector \(b\) is in the range of \(T\text{,}\) you have to solve the matrix equation \(Ax=b\) to see whether it is consistent.
If \(T\colon\mathbb{R}^n \to\mathbb{R}^m \) is an onto matrix transformation, what can we say about the relative sizes of \(n\) and \(m\text{?}\)
The matrix associated to \(T\) has \(n\) columns and \(m\) rows. Each row and each column can only contain one pivot, so in order for \(A\) to have a pivot in every row, it must have at least as many columns as rows: \(m\leq n\).
This says that, for instance, \(\mathbb{R}^2 \) is “too small” to admit an onto linear transformation to \(\mathbb{R}^3 \).
Note that there exist wide matrices that are not onto: for example,
\[\left(\begin{array}{ccc}1&-1&2\\-2&2&-4\end{array}\right)\nonumber\]
does not have a pivot in every row.
Comparison
The above expositions of one-to-one and onto transformations were written to mirror each other. However, “one-to-one” and “onto” are complementary notions: neither one implies the other. Below we have provided a chart for comparing the two. In the chart, \(A\) is an \(m\times n\) matrix, and \(T\colon\mathbb{R}^n \to\mathbb{R}^m \) is the matrix transformation \(T(x)=Ax\).
Table \(\PageIndex{1}\)
| \(T\) is one-to-one | \(T\) is onto |
|---|---|
| \(T(x)=b\) has at most one solution for every \(b\). | \(T(x)=b\) has at least one solution for every \(b\). |
| The columns of \(A\) are linearly independent. | The columns of \(A\) span \(\mathbb{R}^m\). |
| \(A\) has a pivot column in every column. | \(A\) has a pivot in every row. |
| The range of \(T\) has dimension \(n\). | The range of \(T\) has dimension \(m\). |
The function \(\sin\colon \mathbb{R} \to\mathbb{R} \) is neither one-to-one nor onto.
The function \(\exp\colon \mathbb{R} \to\mathbb{R} \) defined by \(\exp(x) = e^x\) is one-to-one but not onto.
The function \(f\colon \mathbb{R} \to\mathbb{R} \) defined by \(f(x)=x^3\) is one-to-one and onto.
The function \(f\colon \mathbb{R} \to\mathbb{R} \) defined by \(f(x)=x^3-x\) is onto but not one-to-one.
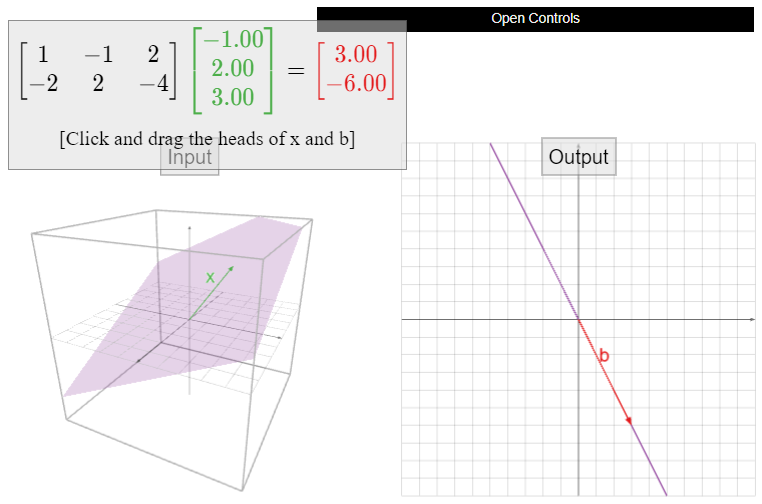
Let
\[A=\left(\begin{array}{ccc}1&-1&2\\-2&2&-4\end{array}\right),\nonumber\]
and define \(T\colon\mathbb{R}^3 \to\mathbb{R}^2 \) by \(T(x) = Ax\). This transformation is neither one-to-one nor onto, as we saw in Example \(\PageIndex{6}\) and Example \(\PageIndex{11}\).
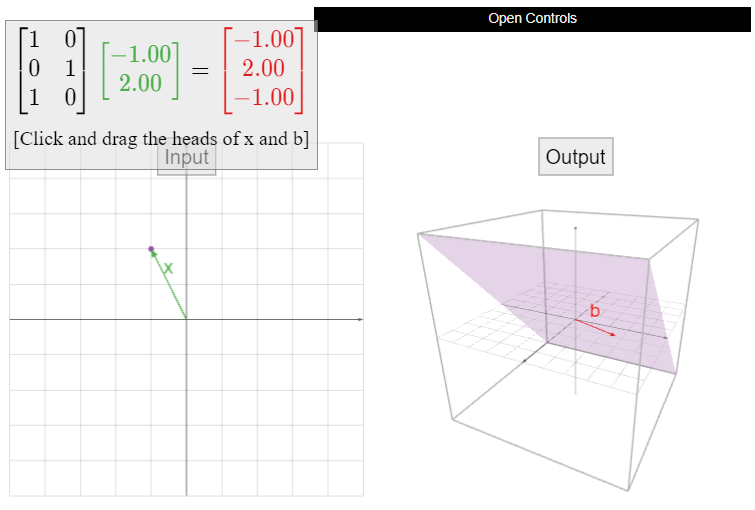
Let \(A\) be the matrix
\[A=\left(\begin{array}{cc}1&0\\0&1\\1&0\end{array}\right),\nonumber\]
and define \(T\colon\mathbb{R}^2 \to\mathbb{R}^3 \) by \(T(x) = Ax\). This transformation is one-to-one but not onto, as we saw in this Example \(\PageIndex{3}\) and this Example \(\PageIndex{10}\).
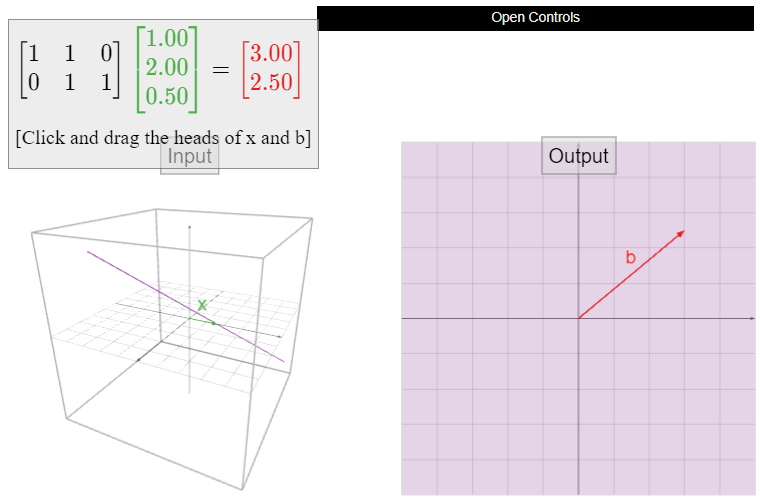
Let \(A\) be the matrix
\[A=\left(\begin{array}{ccc}1&1&0\\0&1&1\end{array}\right),\nonumber\]
and define \(T\colon\mathbb{R}^3 \to\mathbb{R}^2 \) by \(T(x) = Ax\). This transformation is onto but not one-to-one, as we saw in Example \(\PageIndex{9}\).
In Subsection Matrices as Functions in Section 3.1, we discussed the transformations defined by several \(2\times 2\) matrices, namely:
\begin{align*} \text{Reflection:} &\qquad A=\left(\begin{array}{cc}-1&0\\0&1\end{array}\right) \\ \text{Dilation:} &\qquad A=\left(\begin{array}{cc}1.5&0\\0&1.5\end{array}\right) \\ \text{Identity:} &\qquad A=\left(\begin{array}{cc}1&0\\0&1\end{array}\right) \\ \text{Rotation:} &\qquad A=\left(\begin{array}{cc}0&-1\\1&0\end{array}\right) \\ \text{Shear:} &\qquad A=\left(\begin{array}{cc}1&1\\0&1\end{array}\right). \end{align*}
In each case, the associated matrix transformation \(T(x)=Ax\) is both one-to-one and onto. A \(2\times 2\) matrix \(A\) has a pivot in every row if and only if it has a pivot in every column (if and only if it has two pivots), so in this case, the transformation \(T\) is one-to-one if and only if it is onto. One can see geometrically that they are onto (what is the input for a given output?), or that they are one-to-one using the fact that the columns of \(A\) are not collinear.

We observed in the previous Example \(\PageIndex{16}\) that a square matrix has a pivot in every row if and only if it has a pivot in every column. Therefore, a matrix transformation \(T\) from \(\mathbb{R}^n \) to itself is one-to-one if and only if it is onto: in this case, the two notions are equivalent.
Conversely, by Note \(\PageIndex{1}\) and Note \(\PageIndex{2}\), if a matrix transformation \(T\colon\mathbb{R}^m \to\mathbb{R}^n \) is both one-to-one and onto, then \(m=n\).
Note that in general, a transformation \(T\) is both one-to-one and onto if and only if \(T(x)=b\) has exactly one solution for all \(b\) in \(\mathbb{R}^m \).


