9.11: Transforms and Partial Differential Equations

As another application of the transforms, we will see that we can use transforms to solve some linear partial differential equations. We will first solve the one dimensional heat equation and the two dimensional Laplace equations using Fourier transforms. The transforms of the partial differential equations lead to ordinary differential equations which are easier to solve. The final solutions are then obtained using inverse transforms.

We could go further by applying a Fourier transform in space and a Laplace transform in time to convert the heat equation into an algebraic equation. We will also show that we can use a finite sine transform to solve nonhomogeneous problems on finite intervals. Along the way we will identify several Green’s functions.

Fourier Transform and the Heat Equation

We will first consider the solution of the heat equation on an infinite interval using Fourier transforms. The basic scheme has been discussed earlier and is outlined in Figure $\PageIndex{1}$.

Figure $\PageIndex{1}$: Using Fourier transforms to solve a linear partial differential equation.

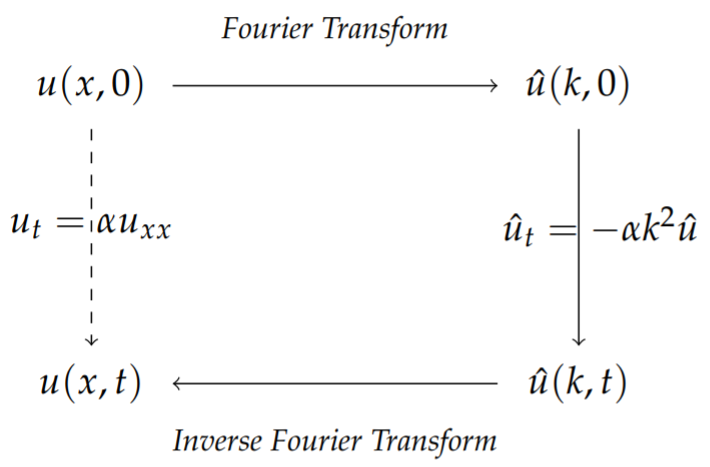
Consider the heat equation on the infinite line,

$$\begin{array}{lr} u_{t}=\alpha u_{x x}, &-\infty<x<\infty, t>0 . \\ u(x, 0)=f(x), & -\infty<x<\infty .\end{array}\label{eq:1}$$

We can Fourier transform the heat equation using the Fourier transform of $u(x, t)$,

$$\mathcal{F}[u(x, t)]=\hat{u}(k, t)=\int_{-\infty}^{\infty} u(x, t) e^{i k x} d x\nonumber$$

We need to transform the derivatives in the equation. First we note that

$$\begin{align} \mathcal{F}\left[u_{t}\right] &=\int_{-\infty}^{\infty} \frac{\partial u(x, t)}{\partial t} e^{i k x} d x\nonumber \\ &=\frac{\partial}{\partial t} \int_{-\infty}^{\infty} u(x, t) e^{i k x} d x\nonumber \\ &=\frac{\partial \hat{u}(k, t)}{\partial t}\label{eq:2} \end{align}$$

Assuming that $\lim _{|x| \rightarrow \infty} u(x, t)=0$ and $\lim _{|x| \rightarrow \infty} u_{x}(x, t)=0$, then we also have that

$$\begin{align} \mathcal{F}\left[u_{x x}\right] &=\int_{-\infty}^{\infty} \frac{\partial^{2} u(x, t)}{\partial x^{2}} e^{i k x} d x\nonumber \\ &=-k^{2} \hat{u}(k, t)\label{eq:3} \end{align}$$

Therefore, the heat equation becomes

$$\frac{\partial \hat{u}(k, t)}{\partial t}=-\alpha k^{2} \hat{u}(k, t)\nonumber$$

This is a first order differential equation which is readily solved as

$$\hat{u}(k, t)=A(k) e^{-\alpha k^{2} t}\nonumber$$

where $A(k)$ is an arbitrary function of $k$. The inverse Fourier transform is

$$\begin{align} u(x, t) &=\frac{1}{2 \pi} \int_{-\infty}^{\infty} \hat{u}(k, t) e^{-i k x} d k\nonumber \\ &=\frac{1}{2 \pi} \int_{-\infty}^{\infty} \hat{A}(k) e^{-\alpha k^{2} t} e^{-i k x} d k\label{eq:4} \end{align}$$

We can determine $A(k)$ using the initial condition. Note that

$$\mathcal{F}[u(x, 0)]=\hat{u}(k, 0)=\int_{-\infty}^{\infty} f(x) e^{i k x} d x .\nonumber$$

But we also have from the solution,

$$u(x, 0)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} \hat{A}(k) e^{-i k x} d k .\nonumber$$

Comparing these two expressions for $\hat{u}(k, 0)$, we see that

$$A(k)=\mathcal{F}[f(x)] .\nonumber$$

We note that $\hat{u}(k, t)$ is given by the product of two Fourier transforms, $\hat{u}(k, t)=A(k) e^{-\alpha k^{2} t}$. So, by the Convolution Theorem, we expect that $u(x, t)$ is the convolution of the inverse transforms,

$$u(x, t)=(f * g)(x, t)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} f(\xi, t) g(x-\xi, t) d \xi,\nonumber$$

where

$$g(x, t)=\mathcal{F}^{-1}\left[e^{-\alpha k^{2} t}\right]\nonumber$$

In order to determine $g(x, t)$, we need only recall Example 9.5.1. In that example we saw that the Fourier transform of a Gaussian is a Gaussian. Namely, we found that

$$\mathcal{F}\left[e^{-a x^{2} / 2}\right]=\sqrt{\frac{2 \pi}{a}} e^{-k^{2} / 2 a},\nonumber$$

or,

$${\mathcal{F}}^{-1}\left[\sqrt{\frac{2 \pi}{a}} e^{-k^{2} / 2 a}\right]=e^{-a x^{2} / 2} .\nonumber$$

Applying this to the current problem, we have

$$g(x)=\mathcal{F}^{-1}\left[e^{-\alpha k^{2} t}\right]=\sqrt{\frac{\pi}{\alpha t}} e^{-x^{2} / 4 t} .\nonumber$$

Finally, we can write down the solution to the problem:

$$u(x, t)=(f * g)(x, t)=\int_{-\infty}^{\infty} f(\xi, t) \frac{e^{-(x-\xi)^{2} / 4 t}}{\sqrt{4 \pi \alpha t}} d \xi,\nonumber$$

The function in the integrand,

$$K(x, t)=\frac{e^{-x^{2} / 4 t}}{\sqrt{4 \pi \alpha t}}\nonumber$$

is called the heat kernel.

Laplace’s Equation on the Half Plane

We consider a steady state solution in two dimensions. In particular, we look for the steady state solution, $u(x, y)$, satisfying the two-dimensional Laplace equation on a semi-infinite slab with given boundary conditions as shown in Figure $\PageIndex{2}$. The boundary value problem is given as

$$\begin{array}{r} u_{x x}+u_{y y}=0, \quad-\infty<x<\infty, \quad y>0, \\ u(x, 0)=f(x), \quad-\infty<x<\infty \\ \lim _{y \rightarrow \infty} u(x, y)=0, \quad \lim _{|x| \rightarrow \infty} u(x, y)=0 . \end{array}\label{eq:5}$$

Figure $\PageIndex{2}$: This is the domain for a semi-infinite slab with boundary value $u(x, 0)=f(x)$ and governed by Laplace’s equation.

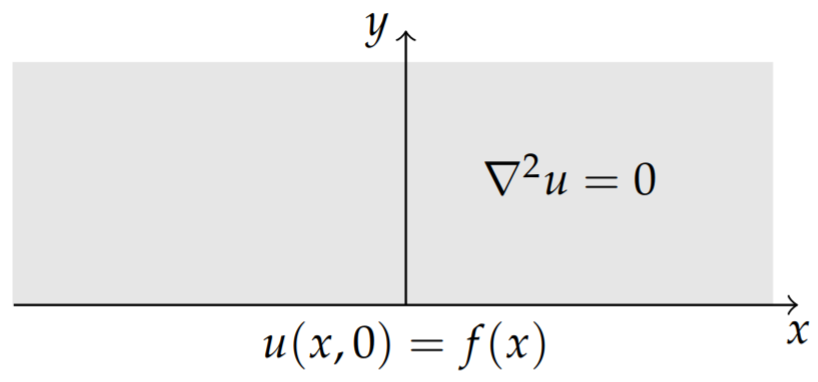
This problem can be solved using a Fourier transform of $u(x, y)$ with respect to $x$. The transform scheme for doing this is shown in Figure $\PageIndex{3}$. We begin by defining the Fourier transform

$$\hat{u}(k, y)=\mathcal{F}[u]=\int_{-\infty}^{\infty} u(x, y) e^{i k x} d x .\nonumber$$

Figure $\PageIndex{3}$: The transform scheme used to convert Laplace’s equation to an ordinary differential equation which is easier to solve.

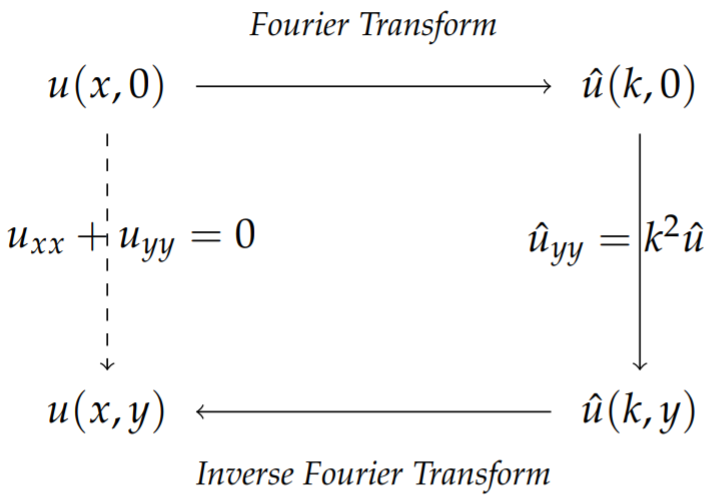
We can transform Laplace’s equation. We first note from the properties of Fourier transforms that

$$\mathcal{F}\left[\frac{\partial^{2} u}{\partial x^{2}}\right]=-k^{2} \hat{u}(k, y),\nonumber$$

if $\lim _{|x| \rightarrow \infty} u(x, y)=0$ and $\lim _{|x| \rightarrow \infty} u_{x}(x, y)=0$. Also,

$$\mathcal{F}\left[\frac{\partial^{2} u}{\partial y^{2}}\right]=\frac{\partial^{2} \hat{u}(k, y)}{\partial y^{2}} .\nonumber$$

Thus, the transform of Laplace’s equation gives $\hat{u}_{y y}=k^{2} \hat{u}$.

This is a simple ordinary differential equation. We can solve this equation using the boundary conditions. The general solution is

$$\hat{u}(k, y)=a(k) e^{k y}+b(k) e^{-k y} .\nonumber$$

Since $\lim _{y \rightarrow \infty} u(x, y)=0$ and $k$ can be positive or negative, we have that $\hat{u}(k, y)=a(k) e^{-|k| y}$. The coefficient $a(k)$ can be determined using the remaining boundary condition, $u(x, 0)=f(x)$. We find that $a(k)=\hat{f}(k)$ since

$$a(k)=\hat{u}(k, 0)=\int_{-\infty}^{\infty} u(x, 0) e^{i k x} d x=\int_{-\infty}^{\infty} f(x) e^{i k x} d x=\hat{f}(k) .\nonumber$$

We have found that $\hat{u}(k, y)=\hat{f}(k) e^{-|k| y}$. We can obtain the solution using the inverse Fourier transform,

$$u(x, t)=\mathcal{F}^{-1}\left[\hat{f}(k) e^{-|k| y]} .\right.\nonumber$$

We note that this is a product of Fourier transforms and use the Convolution Theorem for Fourier transforms. Namely, we have that $a(k)=\mathcal{F}[f]$ and $e^{-|k| y}=\mathcal{F}[g]$ for $g(x, y)=\frac{2 y}{x^{2}+y^{2}}$. This last result is essentially proven in Problem $6 .$

Then, the Convolution Theorem gives the solution

$$\begin{align} u(x, y) &=\frac{1}{2 \pi} \int_{-\infty}^{\infty} f(\xi) g(x-\xi) d \xi\nonumber \\ &=\frac{1}{2 \pi} \int_{-\infty}^{\infty} f(\xi) \frac{2 y}{(x-\xi)^{2}+y^{2}} d \xi\label{eq:6} \end{align}$$

We note for future use, that this solution is in the form

$$u(x, y)=\int_{-\infty}^{\infty} f(\xi) G(x, \xi ; y, 0) d \xi,\nonumber$$

where

$$G(x, \xi ; y, 0)=\frac{2 y}{\pi\left((x-\xi)^{2}+y^{2}\right)}\nonumber$$

is the Green’s function for this problem.

Heat Equation on Infinite Interval, Revisited

We will reconsider the initial value problem for the heat equation on an infinite interval,

$$\begin{array}{lr} u_{t}=u_{x x}, & -\infty<x<\infty, \quad t>0 \\ u(x, 0)=f(x), & -\infty<x<\infty .\end{array}\label{eq:7}$$

We can apply both a Fourier and a Laplace transform to convert this to an algebraic problem. The general solution will then be written in terms of an initial value Green’s function as

$$u(x, t)=\int_{-\infty}^{\infty} G(x, t ; \xi, 0) f(\xi) d \xi .\nonumber$$

For the time dependence we can use the Laplace transform and for the spatial dependence we use the Fourier transform. These combined transforms lead us to define

$$\hat{u}(k, s)=\mathcal{F}[\mathcal{L}[u]]=\int_{-\infty}^{\infty} \int_{0}^{\infty} u(x, t) e^{-s t} e^{i k x} d t d x .\nonumber$$

Applying this to the terms in the heat equation, we have

$$\begin{align} \mathcal{F}\left[\mathcal{L}\left[u_{t}\right]\right] &=s \hat{u}(k, s)-\mathcal{F}[u(x, 0)]\nonumber \\ &=s \hat{u}(k, s)-\hat{f}(k)\nonumber \\ \mathcal{F}\left[\mathcal{L}\left[u_{x x}\right]\right] &=-k^{2} \hat{u}(k, s) .\label{eq:8} \end{align}$$

Here we have assumed that

$$\lim _{t \rightarrow \infty} u(x, t) e^{-s t}=0, \quad \lim _{|x| \rightarrow \infty} u(x, t)=0, \quad \lim _{|x| \rightarrow \infty} u_{x}(x, t)=0 .\nonumber$$

Therefore, the heat equation can be turned into an algebraic equation for the transformed solution,

$$\left(s+k^{2}\right) \hat{u}(k, s)=\hat{f}(k),\nonumber$$

or

$$\hat{u}(k, s)=\frac{\hat{f}(k)}{s+k^{2}} .\nonumber$$

The solution to the heat equation is obtained using the inverse transforms for both the Fourier and Laplace transform. Thus, we have

$$\begin{align} u(x, t) &={\mathcal{F}}^{-1}\left[\mathcal{L}^{-1}[\hat{u}]\right]\nonumber \\ &=\frac{1}{2 \pi} \int_{-\infty}^{\infty}\left(\frac{1}{2 \pi i} \int_{c-i \infty}^{c+\infty} \frac{\hat{f}(k)}{s+k^{2}} e^{s t} d s\right) e^{-i k x} d k .\label{eq:9} \end{align}$$

Since the inside integral has a simple pole at $s=-k^{2}$, we can compute the Bromwich integral by choosing $c>-k^{2}$. Thus,

$$\frac{1}{2 \pi i} \int_{c-i \infty}^{c+\infty} \frac{\hat{f}(k)}{s+k^{2}} e^{s t} d s=\operatorname{Res}\left[\frac{\hat{f}(k)}{s+k^{2}} e^{s t} ; s=-k^{2}\right]=e^{-k^{2} t} \hat{f}(k) .\nonumber$$

Inserting this result into the solution, we have

$$\begin{align} u(x, t) &={\mathcal{F}}^{-1}\left[\mathcal{L}^{-1}[\hat{u}]\right]\nonumber \\ &=\frac{1}{2 \pi} \int_{-\infty}^{\infty} \hat{f}(k) e^{-k^{2} t} e^{-i k x} d k .\label{eq:10} \end{align}$$

This solution is of the form

$$u(x, t)=\mathcal{F}^{-1}[\hat{f} \hat{g}]\nonumber$$

for $\hat{g}(k)=e^{-k^{2} t}$. So, by the Convolution Theorem for Fourier transforms, the solution is a convolution,

$$u(x, t)=\int_{-\infty}^{\infty} f(\xi) g(x-\xi) d \xi\nonumber$$

All we need is the inverse transform of $\hat{g}(k)$.

We note that $\hat{g}(k)=e^{-k^{2} t}$ is a Gaussian. Since the Fourier transform of a Gaussian is a Gaussian, we need only recall Example 9.5.1,

$$\mathcal{F}\left[e^{-a x^{2} / 2}\right]=\sqrt{\frac{2 \pi}{a}} e^{-k^{2} / 2 a} .\nonumber$$

Setting $a=1 / 2 t$, this becomes

$$\mathcal{F}\left[e^{-x^{2} / 4 t}\right]=\sqrt{4 \pi t} e^{-k^{2} t} .\nonumber$$

So,

$$g(x)={\mathcal{F}}^{-1}\left[e^{-k^{2} t}\right]=\frac{e^{-x^{2} / 4 t}}{\sqrt{4 \pi t}}\nonumber$$

Inserting $g(x)$ into the solution, we have

$$\begin{align} u(x, t) &=\frac{1}{\sqrt{4 \pi t}} \int_{-\infty}^{\infty} f(\xi) e^{-(x-\xi)^{2} / 4 t} d \xi\nonumber \\ &=\int_{-\infty}^{\infty} G(x, t ; \zeta, 0) f(\xi) d \xi\label{eq:11} \end{align}$$

Here we have identified the initial value Green’s function

$$G(x, t ; \xi, 0)=\frac{1}{\sqrt{4 \pi t}} e^{-(x-\xi)^{2} / 4 t} .\nonumber$$

Nonhomogeneous Heat Equation

We now consider the nonhomogeneous heat equation with homogeneous boundary conditions defined on a finite interval.

$$\begin{array}{r} u_{t}-k u_{x x}=h(x, t), \quad 0 \leq x \leq L, \quad t>0 \\ u(0, t)=0, \quad u(L, t)=0, \quad t>0 \\ u(x, 0)=f(x), \quad 0 \leq x \leq\end{array}\label{eq:12}$$

We know that when $h(x, t) \equiv 0$ the solution takes the form

$$u(x, t)=\sum_{n=1}^{\infty} b_{n} \sin \frac{n \pi x}{L}\nonumber$$

So, when $h(x, t) \neq 0$, we might assume that the solution takes the form

$$u(x, t)=\sum_{n=1}^{\infty} b_{n}(t) \sin \frac{n \pi x}{L}\nonumber$$

where the $b_{n}^{\prime}$ s are the finite Fourier sine transform of the desired solution,

$$b_{n}(t)=\mathcal{F}_{s}[u]=\frac{2}{L} \int_{0}^{L} u(x, t) \sin \frac{n \pi x}{L} d x\nonumber$$

Note that the finite Fourier sine transform is essentially the Fourier sine transform which we encountered in Section 3.4.

The idea behind using the finite Fourier Sine Transform is to solve the given heat equation by transforming the heat equation to a simpler equation for the transform, $b_{n}(t)$, solve for $b n(t)$, and then do an inverse transform, i.e., insert the $b_{n}(t)$ ’s back into the series representation. This is depicted in Figure $\PageIndex{4}$. Note that we had explored similar diagram earlier when discussing the use of transforms to solve differential equations.

Figure $\PageIndex{4}$: Using finite Fourier transforms to solve the heat equation by solving an ODE instead of a PDE.

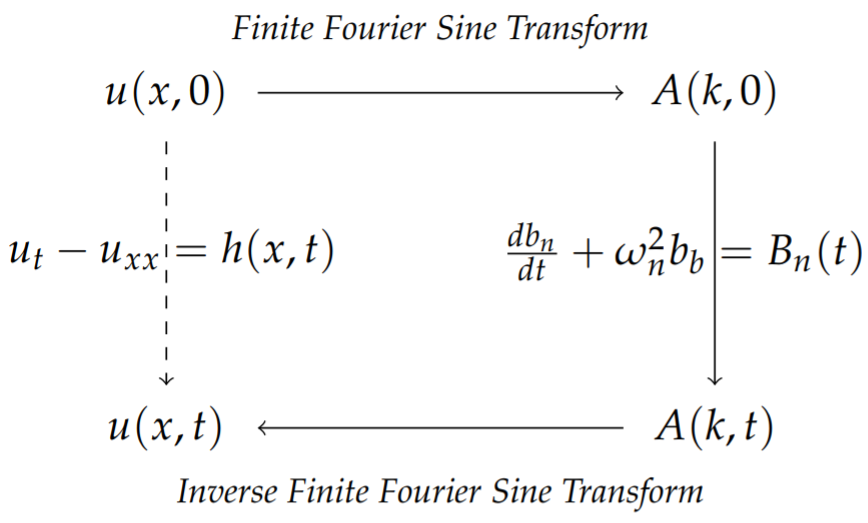
First, we need to transform the partial differential equation. The finite transforms of the derivative terms are given by

$$\begin{align} \mathcal{F}_{s}\left[u_{t}\right]=& \frac{2}{L} \int_{0}^{L} \frac{\partial u}{\partial t}(x, t) \sin \frac{n \pi x}{L} d x\nonumber \\ =& \frac{d}{d t}\left(\frac{2}{L} \int_{0}^{L} u(x, t) \sin \frac{n \pi x}{L} d x\right)\nonumber \\ =& \frac{d b_{n}}{d t} .\label{eq:13}\end{align}$$

$$\begin{align} \mathcal{F}_{s}\left[u_{x x}\right]=& \frac{2}{L} \int_{0}^{L} \frac{\partial^{2} u}{\partial x^{2}}(x, t) \sin \frac{n \pi x}{L} d x\nonumber \\ =&\left[u_{x} \sin \frac{n \pi x}{L}\right]_{0}^{L}-\left(\frac{n \pi}{L}\right) \frac{2}{L} \int_{0}^{L} \frac{\partial u}{\partial x}(x, t) \cos \frac{n \pi x}{L} d x\nonumber \\ =&-\left[\frac{n \pi}{L} u \cos \frac{n \pi x}{L}\right]_{0}^{L}-\left(\frac{n \pi}{L}\right)^{2} \frac{2}{L} \int_{0}^{L} u(x, t) \sin \frac{n \pi x}{L} d x\nonumber \\ =& \frac{n \pi}{L}[u(0, t)-u(L, 0) \cos n \pi]-\left(\frac{n \pi}{L}\right)^{2} b_{n}^{2}\nonumber \\ =&-\omega_{n}^{2} b_{n,}^{2}\label{eq:14} \end{align}$$

where $\omega_{n}=\frac{n \pi}{L}$.

Furthermore, we define

$$H_{n}(t)=\mathcal{F}_{s}[h]=\frac{2}{L} \int_{0}^{L} h(x, t) \sin \frac{n \pi x}{L} d x .\nonumber$$

Then, the heat equation is transformed to

$$\frac{d b_{n}}{d t}+\omega_{n}^{2} b_{n}=H_{n}(t), \quad n=1,2,3, \ldots .\nonumber$$

This is a simple linear first order differential equation. We can supplement this equation with the initial condition

$$b_{n}(0)=\frac{2}{L} \int_{0}^{L} u(x, 0) \sin \frac{n \pi x}{L} d x .\nonumber$$

The differential equation for $b_{n}$ is easily solved using the integrating factor, $\mu(t)=e^{\omega_{n}^{2} t}$. Thus,

$$\frac{d}{d t}\left(e^{\omega_{n}^{2} t} b_{n}(t)\right)=H_{n}(t) e^{\omega_{n}^{2} t}\nonumber$$

and the solution is

$$b_{n}(t)=b_{n}(0) e^{-\omega_{n}^{2} t}+\int_{0}^{t} H_{n}(\tau) e^{-\omega_{n}^{2}(t-\tau)} d \tau\nonumber$$

The final step is to insert these coefficients (finite Fourier sine transform) into the series expansion (inverse finite Fourier sine transform) for $u(x, t)$. The result is

$$u(x, t)=\sum_{n=1}^{\infty} b_{n}(0) e^{-\omega_{n}^{2} t} \sin \frac{n \pi x}{L}+\sum_{n=1}^{\infty}\left[\int_{0}^{t} H_{n}(\tau) e^{-\omega_{n}^{2}(t-\tau)} d \tau\right] \sin \frac{n \pi x}{L} .\nonumber$$

This solution can be written in a more compact form in order to identify the Green’s function. We insert the expressions for $b_{n}(0)$ and $H_{n}(t)$ in terms of the initial profile and source term and interchange sums and integrals. This leads to

$$\begin{align} u(x, t)=& \sum_{n=1}^{\infty}\left(\frac{2}{L} \int_{0}^{L} u(\xi, 0) \sin \frac{n \pi \xi}{L} d \xi\right) e^{-\omega_{n}^{2} t} \sin \frac{n \pi x}{L}\nonumber \\ &+\sum_{n=1}^{\infty}\left[\int_{0}^{t}\left(\frac{2}{L} \int_{0}^{L} h(\xi, \tau) \sin \frac{n \pi \xi}{L} d \xi\right) e^{-\omega_{n}^{2}(t-\tau)} d \tau\right] \sin \frac{n \pi x}{L}\nonumber \\ =& \int_{0}^{L} u(\xi, 0)\left[\frac{2}{L} \sum_{n=1}^{\infty} \sin \frac{n \pi x}{L} \sin \frac{n \pi \xi}{L} e^{-\omega_{n}^{2} t}\right] d \xi\nonumber \\ &+\int_{0}^{t} \int_{0}^{L} h(\xi, \tau)\left[\frac{2}{L} \sum_{n=1}^{\infty} \sin \frac{n \pi x}{L} \sin \frac{n \pi \xi}{L} e^{-\omega_{n}^{2}(t-\tau)}\right]\nonumber \\ =& \int_{0}^{L} u(\xi, 0) G(x, \xi ; t, 0) d \xi+\int_{0}^{t} \int_{0}^{L} h(\xi, \tau) G(x, \xi ; t, \tau) d \xi d \tau\label{eq:15} \end{align}$$

Here we have defined the Green’s function

$$G(x, \xi ; t, \tau)=\frac{2}{L} \sum_{n=1}^{\infty} \sin \frac{n \pi x}{L} \sin \frac{n \pi \xi}{L} e^{-\omega_{n}^{2}(t-\tau)} .\nonumber$$

We note that $G(x, \xi ; t, 0)$ gives the initial value Green’s function.

Note that at $t=\tau$,

$$G(x, \xi ; t, t)=\frac{2}{L} \sum_{n=1}^{\infty} \sin \frac{n \pi x}{L} \sin \frac{n \pi \xi}{L} .\nonumber$$

This is actually the series representation of the Dirac delta function. The Fourier sine transform of the delta function is

$$\mathcal{F}_{s}[\delta(x-\xi)]=\frac{2}{L} \int_{0}^{L} \delta(x-\xi) \sin \frac{n \pi x}{L} d x=\frac{2}{L} \sin \frac{n \pi \xi}{L} .\nonumber$$

Then, the representation becomes

$$\delta(x-\xi)=\frac{2}{L} \sum_{n=1}^{\infty} \sin \frac{n \pi x}{L} \sin \frac{n \pi \xi}{L} .\nonumber$$

Also, we note that

$$\begin{gathered} \frac{\partial G}{\partial t}=-\omega_{n}^{2} G \\ \frac{\partial^{2} G}{\partial x^{2}}=-\left(\frac{n \pi}{L}\right)^{2} G . \end{gathered} \nonumber$$

Therefore, $G_{t}=G_{x x}$ at least for $\tau \neq t$ and $\xi \neq x$.

We can modify this problem by adding nonhomogeneous boundary conditions.

$$\begin{array}{r}u_{t}-k u_{x x}=h(x, t), \quad 0 \leq x \leq L, \quad t>0, \\ u(0, t)=A, \quad u(L, t)=B, \quad t>0, \\ u(x, 0)=f(x), \quad 0 \leq x \leq L .\end{array}\label{eq:16}$$

One way to treat these conditions is to assume $u(x, t)=w(x)+v(x, t)$ where $v_{t}-k v_{x x}=h(x, t)$ and $w_{x x}=0$. Then, $u(x, t)=w(x)+v(x, t)$ satisfies the original nonhomogeneous heat equation.

If $v(x, t)$ satisfies $v(0, t)=v(L, t)=0$ and $w(x)$ satisfies $w(0)=A$ and $w(L)=B$, then $u(0, t)=w(0)+v(0, t)=A u(L, t)=w(L)+v(L, t)=B$

Finally, we note that

$$v(x, 0)=u(x, 0)-w(x)=f(x)-w(x) .\nonumber$$

Therefore, $u(x, t)=w(x)+v(x, t)$ satisfies the original problem if

$$\begin{array}{r} v_{t}-k v_{x x}=h(x, t), \quad 0 \leq x \leq L, \quad t>0, \\ v(0, t)=0, \quad v(L, t)=0, \quad t>0, \\ v(x, 0)=f(x)-w(x), \quad 0 \leq x \leq L . \end{array}\label{eq:17}$$

and

$$\begin{align} w_{x x} =0, & 0 \leq x \leq L,\nonumber \\ w(0) =A, & w(L) =B .\label{eq:18} \end{align}$$

We can solve the last problem to obtain $w(x)=A+\frac{B-A}{L} x$. The solution to the problem for $v(x, t)$ is simply the problem we had solved already in terms of Green’s functions with the new initial condition, $f(x)-A-\frac{B-A}{L} x$.

Solution of the $_{3} D$ Poisson Equation

We recall from electrostatics that the gradient of the electric potential gives the electric field, $\mathrm{E}=-\nabla \phi$. However, we also have from Gauss’ Law for electric fields $\nabla \cdot \mathbf{E}=\frac{\rho}{\epsilon_{0}}$, where $\rho(\mathbf{r})$ is the charge distribution at position $\mathbf{r}$. Combining these equations, we arrive at Poisson’s equation for the electric potential,

$$\nabla^{2} \phi=-\frac{\rho}{\epsilon_{0}} .\nonumber$$

We note that Poisson’s equation also arises in Newton’s theory of gravitation for the gravitational potential in the form $\nabla^{2} \phi=-4 \pi G \rho$ where $\rho$ is the matter density.

We consider Poisson’s equation in the form

$$\nabla^{2} \phi(\mathbf{r})=-4 \pi f(\mathbf{r})\nonumber$$

for $\mathbf{r}$ defined throughout all space. We will seek a solution for the potential function using a three dimensional Fourier transform. In the electrostatic problem $f=\rho(\mathbf{r}) / 4 \pi \epsilon_{0}$ and the gravitational problem has $f=G \rho(\mathbf{r})$

The Fourier transform can be generalized to three dimensions as

$$\hat{\phi}(\mathbf{k})=\int_{V} \phi(\mathbf{r}) e^{i \mathbf{k} \cdot \mathbf{r}} d^{3} r\nonumber$$

where the integration is over all space, $V, d^{3} r=d x d y d z$, and $\mathbf{k}$ is a three dimensional wavenumber, $\mathbf{k}=k_{x} \mathbf{i}+k_{y} \mathbf{j}+k_{z} \mathbf{k}$. The inverse Fourier transform can then be written as

$$\phi(\mathbf{r})=\frac{1}{(2 \pi)^{3}} \int_{V_{k}} \hat{\phi}(\mathbf{k}) e^{-i \mathbf{k} \cdot \mathbf{r}} d^{3} k,\nonumber$$

where $d^{3} k=d k_{x} d k_{y} d k_{z}$ and $V_{k}$ is all of $k$-space.

The Fourier transform of the Laplacian follows from computing Fourier transforms of any derivatives that are present. Assuming that $\phi$ and its gradient vanish for large distances, then

$$\mathcal{F}\left[\nabla^{2} \phi\right]=-\left(k_{x}^{2}+k_{y}^{2}+k_{z}^{2}\right) \hat{\phi}(\mathbf{k}) .\nonumber$$

Defining $k^{2}=k_{x}^{2}+k_{y}^{2}+k_{z}^{2}$, then Poisson’s equation becomes the algebraic equation

$$k^{2} \hat{\phi}(\mathbf{k})=4 \pi \hat{f}(\mathbf{k}) .\nonumber$$

Solving for $\hat{\phi}(\mathbf{k})$, we have

$$\phi(\mathbf{k})=\frac{4 \pi}{k^{2}} \hat{f}(\mathbf{k}) .\nonumber$$

The solution to Poisson’s equation is then determined from the inverse Fourier transform,

$$\phi(\mathbf{r})=\frac{4 \pi}{(2 \pi)^{3}} \int_{V_{k}} \hat{f}(\mathbf{k}) \frac{e^{-i \mathbf{k} \cdot \mathbf{r}}}{k^{2}} d^{3} k .\label{eq:19}$$

First we will consider an example of a point charge (or mass in the gravitational case) at the origin. We will set $f(\mathbf{r})=f_{0} \delta^{3}(\mathbf{r})$ in order to represent a point source. For a unit point charge, $f_{0}=1 / 4 \pi \epsilon_{0}$.

Note

The three dimensional Dirac delta function, $\delta^{3}\left(\mathbf{r}-\mathbf{r}_{0}\right)$.

Here we have introduced the three dimensional Dirac delta function which, like the one dimensional case, vanishes outside the origin and satisfies a unit volume condition,

$$\int_{V} \delta^{3}(\mathbf{r}) d^{3} r=1 .\nonumber$$

Also, there is a sifting property, which takes the form

$$\int_{V} \delta^{3}\left(\mathbf{r}-\mathbf{r}_{0}\right) f(\mathbf{r}) d^{3} r=f\left(\mathbf{r}_{0}\right) .\nonumber$$

In Cartesian coordinates,

$$\begin{gathered} \delta^{3}(\mathbf{r})=\delta(x) \delta(y) \delta(z), \\ \int_{V} \delta^{3}(\mathbf{r}) d^{3} r=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \delta(x) \delta(y) \delta(z) d x d y d z=1, \end{gathered} \nonumber$$

and

$$\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \delta\left(x-x_{0}\right) \delta\left(y-y_{0}\right) \delta\left(z-z_{0}\right) f(x, y, z) d x d y d z=f\left(x_{0}, y_{0}, z_{0}\right)\nonumber$$

One can define similar delta functions operating in two dimensions and $n$ dimensions.

We can also transform the Cartesian form into curvilinear coordinates. From Section 6.9 we have that the volume element in curvilinear coordinates is

$$d^{3} r=d x d y d z=h_{1} h_{2} h_{3} d u_{1} d u_{2} d u_{3},\nonumber$$

where .

This gives

$$\int_{V} \delta^{3}(\mathbf{r}) d^{3} r=\int_{V} \delta^{3}(\mathbf{r}) h_{1} h_{2} h_{3} d u_{1} d u_{2} d u_{3}=1 .\nonumber$$

Therefore,

$$\begin{align} \delta^{3}(\mathbf{r}) &=\frac{\delta\left(u_{1}\right)}{\left|\frac{\partial \mathbf{r}}{\partial u_{1}}\right|} \frac{\delta\left(u_{2}\right)}{\left|\frac{\partial \mathbf{r}}{\partial u_{2}}\right|} \frac{\delta\left(u_{3}\right)}{\left|\frac{\partial \mathbf{r}}{\partial u_{2}}\right|}\nonumber \\ &=\frac{1}{h_{1} h_{2} h_{3}} \delta\left(u_{1}\right) \delta\left(u_{2}\right) \delta\left(u_{3}\right)\label{eq:20} \end{align}$$

So, for cylindrical coordinates,

$$\delta^{3}(\mathbf{r})=\frac{1}{r} \delta(r) \delta(\theta) \delta(z) .\nonumber$$

Example $\PageIndex{1}$

Find the solution of Poisson’s equation for a point source of the form $f(\mathbf{r})=f_{0} \delta^{3}(\mathbf{r})$.

Solution

The solution is found by inserting the Fourier transform of this source into Equation $\eqref{eq:19}$ and carrying out the integration. The transform of $f(\mathbf{r})$ is found as

$$\hat{f}(\mathbf{k})=\int_{V} f_{0} \delta^{3}(\mathbf{r}) e^{i \mathbf{k} \cdot \mathbf{r}} d^{3} r=f_{0} .\nonumber$$

Inserting $\hat{f}(\mathbf{k})$ into the inverse transform in Equation $\eqref{eq:19}$ and carrying out the integration using spherical coordinates in $k$-space, we find

$$\begin{align} \phi(\mathbf{r}) &=\frac{4 \pi}{(2 \pi)^{3}} \int_{V_{k}} f_{0} \frac{e^{-i \mathbf{k} \cdot \mathbf{r}}}{k^{2}} d^{3} k\nonumber \\ &=\frac{f_{0}}{2 \pi^{2}} \int_{0}^{2 \pi} \int_{0}^{\pi} \int_{0}^{\infty} \frac{e^{-i k x \cos \theta}}{k^{2}} k^{2} \sin \theta d k d \theta d \phi\nonumber \\ &=\frac{f_{0}}{\pi} \int_{0}^{\pi} \int_{0}^{\infty} e^{-i k x \cos \theta} \sin \theta d k d \theta\nonumber \\ &=\frac{f_{0}}{\pi} \int_{0}^{\infty} \int_{-1}^{1} e^{-i k x y} d k d y, \quad y=\cos \theta\nonumber \\ &=\frac{2 f_{0}}{\pi r} \int_{0}^{\infty} \frac{\sin z}{z} d z=\frac{f_{0}}{r}\label{eq:21} \end{align}$$

If the last example is applied to a unit point charge, then $f_{0}=1 / 4 \pi \epsilon_{0}$. So, the electric potential outside a unit point charge located at the origin becomes

$$\phi(\mathbf{r})=\frac{1}{4 \pi \epsilon_{0} r} .\nonumber$$

This is the form familiar from introductory physics.

Also, by setting $f_{0}=1$, we have also shown in the last example that

$$\nabla^{2}\left(\frac{1}{r}\right)=-4 \pi \delta^{3}(\mathbf{r}) \text {. }\nonumber$$

Since $\nabla\left(\frac{1}{r}\right)=-\frac{\mathrm{r}}{r^{3}}$, then we have also shown that

$$\nabla \cdot\left(\frac{\mathbf{r}}{r^{3}}\right)=4 \pi \delta^{3}(\mathbf{r}) \text {. }\nonumber$$